
分析 根据正弦定理余弦定理和基本不等式即可证明$\frac{sinA}{sinA+sinB}$+$\frac{sinC}{sinB+sinC}$=1是∠B≤60°的充分条件,举反例即可说明不是必要条件.
解答 证明:根据正弦定理,$\frac{sinA}{sinA+sinB}$+$\frac{sinC}{sinB+sinC}$=$\frac{a}{a+b}$+$\frac{c}{b+c}$=1,
∴a(b+c)+c(a+b)=(a+b)(b+c),
∴b2=ac,
根据余弦定理,得cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$=$\frac{{a}^{2}+{c}^{2}-ac}{2ac}$≥$\frac{2ac-ac}{2ac}$=$\frac{1}{2}$,当且仅当a=c是取等号,
∵0<B<180°,
∴∠B≤60°,
∴$\frac{sinA}{sinA+sinB}$+$\frac{sinC}{sinB+sinC}$=1是∠B≤60°的充分条件,
当A=90°,C=30°,B=60°时,
$\frac{sinA}{sinA+sinB}$+$\frac{sinC}{sinB+sinC}$=$\frac{1}{1+\frac{\sqrt{3}}{2}}$+$\frac{\frac{1}{2}}{\frac{1}{2}+\frac{\sqrt{3}}{2}}$=4-2$\sqrt{3}$+2($\sqrt{3}$-1)=2≠1,
∴$\frac{sinA}{sinA+sinB}$+$\frac{sinC}{sinB+sinC}$=1是∠B≤60°的充分不必要条件
点评 本题借助于充要条件,考查了正弦定理,余弦定理,基本不等式,属于中档题.


 小学课时特训系列答案
小学课时特训系列答案科目:高中数学 来源: 题型:解答题
 在平行四边形ABCD中,∠CBD=90°,BC=BD=1,将平行四边形沿对角线BD折成60°的二面角(如图中实线部分).求:
在平行四边形ABCD中,∠CBD=90°,BC=BD=1,将平行四边形沿对角线BD折成60°的二面角(如图中实线部分).求:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 正三棱柱ABC一A1B1C1的底面边长为2,D为AB上一点,如图,建立空间直角坐标系.
正三棱柱ABC一A1B1C1的底面边长为2,D为AB上一点,如图,建立空间直角坐标系.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 12 | B. | 20 | C. | 16 | D. | 32 |
查看答案和解析>>
科目:高中数学 来源:2016-2017学年河北冀州市高二文上月考三数学试卷(解析版) 题型:解答题
从一条生产线上每隔30分钟取一件产品,共取了 件,测得其产品尺寸后,画出其频率分布直方图如图,已知尺寸在
件,测得其产品尺寸后,画出其频率分布直方图如图,已知尺寸在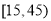 内的频数为92.
内的频数为92.

(Ⅰ)求 的值;
的值;
(Ⅱ)求尺寸在 内产品的个数;
内产品的个数;
(Ⅲ)估计尺寸大于25的频率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com