
【题目】已知函数![]() ,其中
,其中![]()
(Ⅰ)若函数![]() 存在相同的零点,求
存在相同的零点,求![]() 的值;
的值;
(Ⅱ)若存在两个正整数![]() ,当
,当![]() 时,有
时,有![]() 与
与![]() 同时成立,求
同时成立,求![]() 的最大值及
的最大值及![]() 取最大值时
取最大值时![]() 的取值范围.
的取值范围.
 通城学典默写能手系列答案
通城学典默写能手系列答案科目:高中数学 来源: 题型:
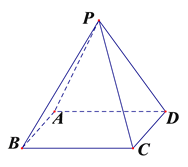
【题目】如图在四棱锥P-ABCD中,底面ABCD为矩形,侧面PAD![]() 底面ABCD,
底面ABCD, ![]() ;
;
(1)求证:平面PAB![]() 平面PCD;
平面PCD;
(2)若过点B的直线![]() 垂直平面PCD,求证:
垂直平面PCD,求证: ![]() //平面PAD.
//平面PAD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是由正整数组成的无穷数列,该数列前
是由正整数组成的无穷数列,该数列前![]() 项的最大值记为
项的最大值记为![]() ,第
,第![]() 项之后各项
项之后各项![]() ,
, ![]() ,
, ![]() 的最小值记为
的最小值记为![]() ,
, ![]() .
.
(I)若![]() 为
为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,是一个周期为
,是一个周期为![]() 的数列(即对任意
的数列(即对任意![]() ,
, ![]() ),写出
),写出![]() ,
, ![]() ,
, ![]() ,
, ![]() 的值.
的值.
(II)设![]() 是正整数,证明:
是正整数,证明: ![]() 的充分必要条件为
的充分必要条件为![]() 是公比为
是公比为![]() 的等比数列.
的等比数列.
(III)证明:若![]() ,
, ![]() ,则
,则![]() 的项只能是
的项只能是![]() 或者
或者![]() ,且有无穷多项为
,且有无穷多项为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合![]() ,其中
,其中![]() ,由
,由![]() 中的元素构成两个相应的集合:
中的元素构成两个相应的集合:
![]() ,
, ![]() .
.
其中![]() 是有序数对,集合
是有序数对,集合![]() 和
和![]() 中的元素个数分别为
中的元素个数分别为![]() 和
和![]() .
.
若对于任意的![]() ,总有
,总有![]() ,则称集合
,则称集合![]() 具有性质
具有性质![]() .
.
(Ⅰ)检验集合![]() 与
与![]() 是否具有性质
是否具有性质![]() 并对其中具有性质
并对其中具有性质![]() 的集合,写出相应的集合
的集合,写出相应的集合![]() 和
和![]() .
.
(Ⅱ)对任何具有性质![]() 的集合
的集合![]() ,证明
,证明![]() .
.
(Ⅲ)判断![]() 和
和![]() 的大小关系,并证明你的结论.
的大小关系,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
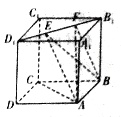
【题目】如图所示,正方体![]() 的棱长为1,线段
的棱长为1,线段![]() 上有两个动点
上有两个动点![]() ,则下列结论中正确结论的序号是__________.
,则下列结论中正确结论的序号是__________.
①![]() ;
;
②直线![]() 与平面
与平面![]() 所成角的正弦值为定值
所成角的正弦值为定值![]() ;
;
③当![]() 为定值,则三棱锥
为定值,则三棱锥![]() 的体积为定值;
的体积为定值;
④异面直线![]() 所成的角的余弦值为定值
所成的角的余弦值为定值![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com