
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,已知曲线
中,已知曲线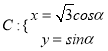 (
(![]() 为参数),在以原点
为参数),在以原点![]() 为极点,
为极点, ![]() 轴的非负半轴为极轴建立的机坐标系中,直线
轴的非负半轴为极轴建立的机坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)过点![]() 且与直线
且与直线![]() 平行的直线
平行的直线![]() 交
交![]() 于
于![]() 两点,求点
两点,求点![]() 到
到![]() 两点的距离之积.
两点的距离之积.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ).
).
(1)若![]() ,求曲线
,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)若不等式![]() 对任意
对任意![]() 恒成立.(i)求实数
恒成立.(i)求实数![]() 的取值范围;(ii)试比较
的取值范围;(ii)试比较![]() 与
与![]() 的大小,并给出证明(
的大小,并给出证明(![]() 为自然对数的底数,
为自然对数的底数, ![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年某招聘会上,有5个条件很类似的求职者,把他们记为A,B,C,D,E,他们应聘秘书工作,但只有2个秘书职位,因此5人中仅有2人被录用,如果5个人被录用的机会相等,分别计算下列事件的概率:
(1)C得到一个职位
(2)B或E得到一个职位.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假设关于某设备的使用年限x和所支出的维修费用y(万元),有如下的统计数据(xi , yi)(i=1,2,3,4,5)由资料知y对x呈线性相关,并且统计的五组数据得平均值分别为 ![]() ,
, ![]() ,若用五组数据得到的线性回归方程
,若用五组数据得到的线性回归方程 ![]() =bx+a去估计,使用8年的维修费用比使用7年的维修费用多1.1万元,
=bx+a去估计,使用8年的维修费用比使用7年的维修费用多1.1万元,
(1)求回归直线方程;
(2)估计使用年限为10年时,维修费用是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的首项a1=1,公差d>0,且第2项、第5项、第14项分别是等比数列{bn}的第2项、第3项、第4项.
(1)求数列{an}与{bn}的通项公式;
(2)设数列{cn}对n∈N*均有 ![]() =an+1成立,求c1+c2+c3+…+c2016 .
=an+1成立,求c1+c2+c3+…+c2016 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校大一新生中的6名同学打算参加学校组织的“演讲团”、“吉他协会”等五个社团,若每名同学必须参加且只能参加1个社团且每个社团至多两人参加,则这6个人中没有人参加“演讲团”的不同参加方法数为( )
A. 3600 B. 1080 C. 1440 D. 2520
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com