
【题目】如图,已知PA⊥平面ABCD,且四边形ABCD为矩形,M、N分别是AB、PC的中点.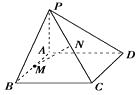
(1)求证:MN⊥CD;
(2)若∠PDA=45°,求证:MN⊥平面PCD.
【答案】
(1)证明:如图所示,取PD的中点E,连接AE、NE,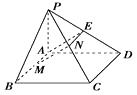
∵N为PC的中点,E为PD的中点,∴NE∥CD且NE= ![]() CD,而AM∥CD
CD,而AM∥CD
且AM= ![]() AB=
AB= ![]() CD,∴NE∥AM且NE=AM,∴四边形AMNE为平行四边形,
CD,∴NE∥AM且NE=AM,∴四边形AMNE为平行四边形,
∴MN∥AE.又PA⊥平面ABCD,∴PA⊥CD,又∵ABCD为矩形,∴AD⊥CD,又AD∩PA=A,∴CD⊥平面PAD,∴CD⊥AE,又AE∥MN,∴MN⊥CD
(2)证明:由(1)可知CD⊥AE,MN∥AE.又∠PDA=45°,∴△PAD为等腰直角三角形,又E为PD的中点,∴AE⊥PD,∴AE⊥平面PCD. 又AE∥MN,∴MN⊥平面PCD
【解析】(1)通过证明CD⊥平面PAD即线面垂直来证明MN⊥CD即线线垂直。
(2)当∠PDA=45°时,△PAD为等腰直角三角形,在平面内找到两条直线都与MN垂直即可。
【考点精析】通过灵活运用直线与平面垂直的判定和直线与平面垂直的性质,掌握一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想;垂直于同一个平面的两条直线平行即可以解答此题.


科目:高中数学 来源: 题型:
【题目】如图, ![]() 是圆柱的母线,
是圆柱的母线, ![]() 是
是 ![]() 的直径,
的直径, ![]() 是底面圆周上异于
是底面圆周上异于 ![]() 的任意一点,
的任意一点, ![]() ,
, ![]() .
.
(1)求证: ![]()
(2)当三棱锥 ![]() 的体积最大时,求
的体积最大时,求 ![]() 与平面
与平面 ![]() 所成角的大小;
所成角的大小;
(3)![]() 上是否存在一点
上是否存在一点 ![]() ,使二面角
,使二面角 ![]() 的平面角为45°?若存在,求出此时
的平面角为45°?若存在,求出此时 ![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB=AC=1,AA1=2,∠B1A1C1=90°,D为BB1的中点.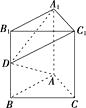
求证:AD⊥平面A1DC1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是R上的奇函数,且当x>0时,f(x)=-2x2+4x+3.
(1)求f(x)的表达式;
(2)画出f(x)的图象,并指出f(x)的单调区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有2名男生和3名女生. (Ⅰ)若其中2名男生必须相邻排在一起,则这5人站成一排,共有多少种不同的排法?
(Ⅱ)若男生甲既不能站排头,也不能站排尾,这5人站成一排,共有多少种不同的排法?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E: ![]() =1的离心率为
=1的离心率为 ![]() ,点F1 , F2是椭圆E的左、右焦点,过F1的直线与椭圆E交于A,B两点,且△F2AB的周长为8.
,点F1 , F2是椭圆E的左、右焦点,过F1的直线与椭圆E交于A,B两点,且△F2AB的周长为8.
(1)求椭圆E的标准方程;
(2)动点M在椭圆E上,动点N在直线l:y=2 ![]() 上,若OM⊥ON,探究原点O到直线MN的距离是否为定值,并说明理由.
上,若OM⊥ON,探究原点O到直线MN的距离是否为定值,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com