
已知两曲线参数方程分别为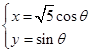 (0≤θ<π)和
(0≤θ<π)和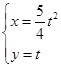 ( t ∈R),求它们的交点坐标.
( t ∈R),求它们的交点坐标.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
已知圆 的参数方程为
的参数方程为 (
( 为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,圆
为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,圆 的极坐标方程为
的极坐标方程为 .
.
(1)将圆 的参数方程化为普通方程,将圆
的参数方程化为普通方程,将圆 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(2)圆 ,
, 是否相交?若相交,请求出公共弦长,若不相交,请说明理由.
是否相交?若相交,请求出公共弦长,若不相交,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(考生注意:只能从A,B,C中选择一题作答,并将答案填写在相应字母后的横线上,若多做,则按所做的第一题评阅给分.)
A.选修4-1:几何证明选讲
已知Rt△ABC的两条直角边AC,BC的长分别为3cm,4cm,以AC为直径的圆与AB交于点D,则BD的值为____.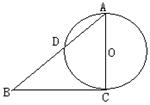
B.选修4-4:坐标系与参数方程
在极坐标系中,已知圆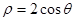 与直线
与直线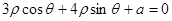 相切,求实数a的值______.
相切,求实数a的值______.
C.选修4-5:不等式选讲
不等式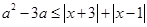 对任意实数
对任意实数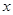 恒成立,求实数
恒成立,求实数 的取值范围____.
的取值范围____.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知P为半圆C: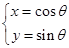 (
(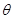 为参数,
为参数,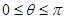 )上的点,点A的坐标为(1,0),
)上的点,点A的坐标为(1,0),
O为坐标原点,点M在射线OP上,线段OM与C的弧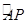 的长度均为
的长度均为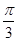 。
。
(Ⅰ)以O为极点, 轴的正半轴为极轴建立极坐标系,求点M的极坐标;
轴的正半轴为极轴建立极坐标系,求点M的极坐标;
(Ⅱ)求直线AM的参数方程。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分10分)(选修4-4:坐标系与参数方程)
在直角坐标系中,直线 的参数方程为
的参数方程为
 为参数).若以坐标原点
为参数).若以坐标原点 为极点,
为极点, 轴正半轴为极轴建立极坐标系,则曲线
轴正半轴为极轴建立极坐标系,则曲线 的极坐标方程为
的极坐标方程为 .
.
(I)求曲线 的直角坐标方程;
的直角坐标方程;
(II)求直线 被曲线
被曲线 所截得的弦长.
所截得的弦长.
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
有人收集了春节期间平均气温x与某取暖商品销售额y的有关数据如下表:
| 平均气温(℃) | ﹣2 | ﹣3 | ﹣5 | ﹣6 |
| 销售额(万元) | 20 | 23 | 27 | 30 |
 x+a的系数
x+a的系数 .则预测平均气温为﹣8℃时该商品销售额为( )
.则预测平均气温为﹣8℃时该商品销售额为( )查看答案和解析>>
科目:高中数学 来源: 题型:单选题
甲、乙、丙、丁四人参加某运动会射击项目选拔赛,四人的平均成绩和方差如下表所示:
| | 甲 | 乙 | 丙 | 丁 |
| 平均环数x | 8.3 | 8.8 | 8.8 | 8.7 |
| 方差s2 | 3.5 | 3.6 | 2.2 | 5.4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com