
【题目】在如图所示的数阵中每一行从左到右均是首项为1,项数为n的等差数列,设第![]() 行的等差数列中的第k项为
行的等差数列中的第k项为![]() 2,3,
2,3,![]() ,
,![]() ,公差为
,公差为![]() ,若
,若![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 也成等差数列.
也成等差数列.
![]() Ⅰ
Ⅰ![]() 求
求![]() ;
;
![]() Ⅱ
Ⅱ![]() 求
求![]() 关于m的表达式;
关于m的表达式;
![]() Ⅲ
Ⅲ![]() 若数阵中第i行所有数之和
若数阵中第i行所有数之和![]() ,第j列所有数之和为
,第j列所有数之和为![]() ,是否存在i,j满足
,是否存在i,j满足![]() ,使得
,使得![]() 成立?若存在,请求出i,j的一组值;若不存在,请说明理由.
成立?若存在,请求出i,j的一组值;若不存在,请说明理由.
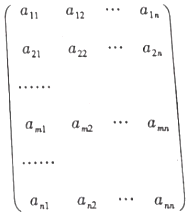
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() ,
,![]() 其中
其中![]() ;(Ⅲ)不存在.
;(Ⅲ)不存在.
【解析】
本题的数阵中蕴涵着很多个等差数列,包括每一行都成等差数列,最后一列也成等差数列,每一行的公差也成等差数列,把握住这些,然后细心运算.
解:![]() Ⅰ
Ⅰ![]() 由题意,可知:
由题意,可知:
![]() 数阵中的第1行是以
数阵中的第1行是以![]() 为首项,
为首项,![]() 为公差的等差数列,
为公差的等差数列,
![]() 数阵中的第1行的最后一项
数阵中的第1行的最后一项![]() .
.
又![]() 数阵中的第2行是以
数阵中的第2行是以![]() 为首项,
为首项,![]() 为公差的等差数列,
为公差的等差数列,
![]() 数阵中的第2行的最后一项
数阵中的第2行的最后一项![]() .
.
![]() 数阵中的每行的最后一项
数阵中的每行的最后一项![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 也成等差数列.
也成等差数列.
![]() .
.
![]() Ⅱ
Ⅱ![]() 由
由![]() Ⅰ
Ⅰ![]() 可知:
可知:
![]() ,
,![]() .
.
数阵中的每行的最后一项![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 是以
是以![]() 为首项,
为首项,![]() 为公差的等差数列.
为公差的等差数列.
![]() 等差数列
等差数列![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 中的第m项
中的第m项![]() .
.
![]() 数阵第m行中第1项
数阵第m行中第1项![]() ,最后一项第n项
,最后一项第n项![]() ,而数阵第m行也是等差数列.
,而数阵第m行也是等差数列.
![]() 数阵第m行的公差
数阵第m行的公差![]() .
.
![]() ,
,![]() 其中
其中![]() .
.
![]() Ⅲ
Ⅲ![]() 由题意及
由题意及![]() Ⅰ
Ⅰ![]() Ⅱ
Ⅱ![]() ,可知:
,可知:
数阵中第i行是以![]() 为首项,
为首项,![]() 为公差的等差数列.
为公差的等差数列.
![]() .
.
由![]() Ⅱ
Ⅱ![]() 可知:
可知:
![]() 是以1为首项,2为公差的等差数列.
是以1为首项,2为公差的等差数列.
![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
等差数列![]() .
.
假设![]() 成立,即
成立,即![]() .
.
整理,得:![]()
要使此式成立,必须有:
![]() ,
,
解得:![]() ,
,![]() 很明显,这与题中条件
很明显,这与题中条件![]() 相矛盾.
相矛盾.
![]() 不存在i,j的一组值,使得
不存在i,j的一组值,使得![]() 成立.
成立.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() ,若x1,x2∈R,且x1≠x2,使得f(x1)=f(x2),则实数a的取值范围是( )
,若x1,x2∈R,且x1≠x2,使得f(x1)=f(x2),则实数a的取值范围是( )
A. [2,3]∪(﹣∞,﹣5]B. (﹣∞,2)∪(3,5)
C. [2,3]D. [5,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某品种一批树苗生长情况,在该批树苗中随机抽取了容量为120的样本,测量树苗高度(单位:cm),经统计,其高度均在区间[19,31]内,将其按[19,21),[21,23),[23,25),[25,27),[27,29),[29,31]分成6组,制成如图所示的频率分布直方图.其中高度为27 cm及以上的树苗为优质树苗.
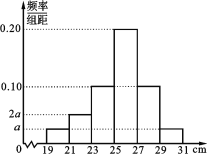
(1)求图中a的值;
(2)已知所抽取的这120棵树苗来自于A,B两个试验区,部分数据如下列联表:
A试验区 | B试验区 | 合计 | |
优质树苗 | 20 | ||
非优质树苗 | 60 | ||
合计 |
将列联表补充完整,并判断是否有99.9%的把握认为优质树苗与A,B两个试验区有关系,并说明理由;
(3)用样本估计总体,若从这批树苗中随机抽取4棵,其中优质树苗的棵数为X,求X的分布列和数学期望EX.
下面的临界值表仅供参考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:![]() ,其中
,其中![]() .)
.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
某位同学进行寒假社会实践活动,为了对白天平均气温与某奶茶店的某种饮料销量之间的关系进行分析研究,他分别记录了1月11日至1月15日的白天平均气温![]() (°C)与该奶茶店的这种饮料销量
(°C)与该奶茶店的这种饮料销量![]() (杯),得到如下数据:
(杯),得到如下数据:
日 期 | 1月11日 | 1月12日 | 1月13日 | 1月14日 | 1月15日 |
平均气温 | 9 | 10 | 12 | 11 | 8 |
销量 | 23 | 25 | 30 | 26 | 21 |
(1)若从这五组数据中随机抽出2组,求抽出的2组数据恰好是相邻2天数据的概率;
(2)请根据所给五组数据,求出y关于x的线性回归方程![]() .
.
(参考公式: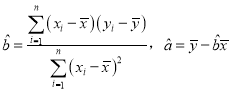 .)
.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年10月28日,重庆公交车坠江事件震惊全国,也引发了广大群众的思考——如何做一个文明的乘客.全国各地大部分社区组织居民学习了文明乘车规范.![]() 社区委员会针对居民的学习结果进行了相关的问卷调查,并将得到的分数整理成如图所示的统计图.
社区委员会针对居民的学习结果进行了相关的问卷调查,并将得到的分数整理成如图所示的统计图.

(Ⅰ)求得分在![]() 上的频率;
上的频率;
(Ⅱ)求![]() 社区居民问卷调查的平均得分的估计值;(同一组中的数据以这组数据所在区间中点的值作代表)
社区居民问卷调查的平均得分的估计值;(同一组中的数据以这组数据所在区间中点的值作代表)
(Ⅲ)以频率估计概率,若在全部参与学习的居民中随机抽取5人参加问卷调查,记得分在![]() 间的人数为
间的人数为![]() ,求
,求![]() 的分布列.
的分布列.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com