
【题目】已知直线l过点P(0,﹣4),且倾斜角为 ![]() ,圆C的极坐标方程为ρ=4cosθ.
,圆C的极坐标方程为ρ=4cosθ.
(1)求直线l的参数方程和圆C的直角坐标方程;
(2)若直线l和圆C相交于A、B两点,求|PA||PB|及弦长|AB|的值.
【答案】
(1)解:直线l的参数方程为 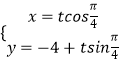 (t为参数),即
(t为参数),即 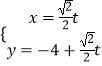 (t为参数).
(t为参数).
圆C的极坐标方程为ρ=4cosθ,即ρ2=4ρcosθ,∴圆C的直角坐标方程为:x2+y2=4x
(2)解:把直线l的参数方程代入圆C的方程,化简得 ![]() +16=0,
+16=0,
△>0,∴t1t2=16,t1+t2=6 ![]() .
.
∴|PA||PB|=|t1t2|=16,
弦长|AB|=|t1﹣t2|= ![]() =
= ![]() =2
=2 ![]()
【解析】(1)直线l的参数方程为 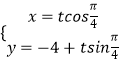 (t为参数),化简即可得出.圆C的极坐标方程为ρ=4cosθ,即ρ2=4ρcosθ,利用互化公式即可得出圆C的直角坐标方程.(2)把直线l的参数方程代入圆C的方程,化简得
(t为参数),化简即可得出.圆C的极坐标方程为ρ=4cosθ,即ρ2=4ρcosθ,利用互化公式即可得出圆C的直角坐标方程.(2)把直线l的参数方程代入圆C的方程,化简得 ![]() +16=0,利用根与系数的关系及其:|PA||PB|=|t1t2|,弦长|AB|=|t1﹣t2|=
+16=0,利用根与系数的关系及其:|PA||PB|=|t1t2|,弦长|AB|=|t1﹣t2|= ![]() ,即可得出.
,即可得出.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】定义:在平面内,点![]() 到曲线
到曲线![]() 上的点的距离的最小值称为点
上的点的距离的最小值称为点![]() 到曲线
到曲线![]() 的距离,在平面直角坐标系
的距离,在平面直角坐标系![]() 中,已知圆
中,已知圆![]() :
: ![]() 及点
及点![]() ,动点
,动点![]() 到圆
到圆![]() 的距离与到
的距离与到![]() 点的距离相等,记
点的距离相等,记![]() 点的轨迹为曲线
点的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)过原点的直线![]() (
(![]() 不与坐标轴重合)与曲线
不与坐标轴重合)与曲线![]() 交于不同的两点
交于不同的两点![]() ,点
,点![]() 在曲线
在曲线![]() 上,且
上,且![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,设直线
,设直线![]() 的斜率分别为
的斜率分别为![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知具有相关关系的两个变量![]() 之间的几组数据如下表所示:
之间的几组数据如下表所示:

(1)请根据上表数据在网格纸中绘制散点图;
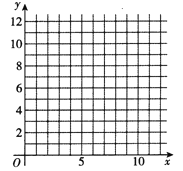
(2)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并估计当
,并估计当![]() 时,
时, ![]() 的值;
的值;
(3)将表格中的数据看作五个点的坐标,则从这五个点中随机抽取3个点,记落在直线![]() 右下方的点的个数为
右下方的点的个数为![]() ,求
,求![]() 的分布列以及期望.
的分布列以及期望.
参考公式: 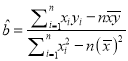 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的离心率为
的离心率为![]() ,且椭圆
,且椭圆![]() 过点
过点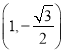 ,记椭圆
,记椭圆![]() 的左、右顶点分别为
的左、右顶点分别为![]() ,点
,点![]() 是椭圆
是椭圆![]() 上异于
上异于![]() 的点,直线
的点,直线![]() 与直线
与直线![]() 分别交于点
分别交于点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 作椭圆
作椭圆![]() 的切线
的切线![]() ,记
,记![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)为二次函数,且f(x﹣1)+f(x)=2x2+4.
(1)求f(x)的解析式;
(2)当x∈[t,t+2],t∈R时,求函数f(x)的最小值(用t表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com