
当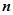 为正整数时,定义函数
为正整数时,定义函数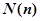 表示
表示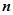 的最大奇因数.如
的最大奇因数.如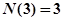 ,
,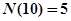 ,….记
,….记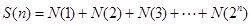 .则
.则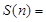 .(用
.(用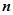 来表示)
来表示)
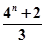
【解析】
试题分析:由N(x)的性质可得知,当x是奇数时,x的最大奇数因子明显是它本身.因此N(x)=x,因此,我们就可将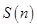 进行分解,分别算出奇数项的和与偶数项的和进而相加,即
进行分解,分别算出奇数项的和与偶数项的和进而相加,即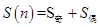 ,
,
所以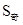 =N(1)+N(3)+…+N(
=N(1)+N(3)+…+N(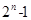 )=1+3+…+
)=1+3+…+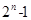 =
= 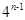 。
。
当x是偶数时,且x∈[ )
)
①当k=1时,x∈[2,4)该区间包含的偶数只有2,而N(2)=1所以该区间所有的偶数的最大奇因数之和为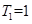 ;
;
②当k=2时,x∈[4,8),该区间包含的偶数为4,6,所以该区间所有的最大奇因数偶数之和为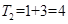
③当k=3时,x∈[8,16),该区间包含的偶数为8,10.,12,14,则该区间所有偶数的最大奇因数之和为 ,因此我们可以用数学归纳法得出当x∈[
,因此我们可以用数学归纳法得出当x∈[ )该区间所有偶数的最大奇因数和
)该区间所有偶数的最大奇因数和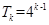
∴对k从1到n-1求和得
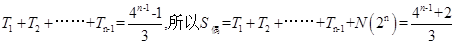 ,
,
综上知: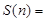
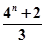 。
。
考点:数列的综合应用。
点评:本题主要考查了数列的求和问题.考查了学生通过已知条件分析问题和解决问题的能力.


科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com