
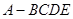 的侧面
的侧面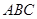 是等边三角形,
是等边三角形,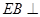 平面
平面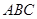 ,
,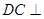 平面
平面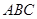 ,
,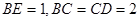 ,
,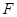 是棱
是棱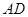 的中点.
的中点.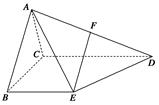
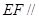 平面
平面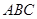 ;
;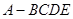 的体积.
的体积.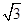
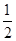 DC=1,
DC=1,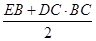 =3,
=3,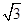 ,∴V棱锥A-BCDE=
,∴V棱锥A-BCDE=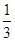 S梯形BCDE·AN=
S梯形BCDE·AN=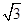 .
.

 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案科目:高中数学 来源:不详 题型:解答题
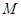 、
、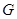 分别是
分别是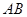 、
、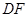 的中点.
的中点.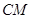
 平面
平面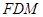
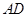 上(含
上(含 、
、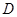 端点)确定一点
端点)确定一点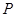 ,使得
,使得
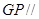 平面
平面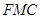 ,并给出证明;
,并给出证明;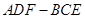 内自由飞,求它飞入几何体
内自由飞,求它飞入几何体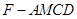 内的概率.
内的概率. 
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 底面
底面 为菱形,
为菱形, 平面
平面 ,
, ,
, 分别是
分别是 、
、 的中点.
的中点. 
 , 若
, 若 为线段
为线段 上的动点,
上的动点, 与平面
与平面 所成的最大角的正切值为
所成的最大角的正切值为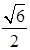 ,求此时异面直线AE和CH所成的角.
,求此时异面直线AE和CH所成的角.
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
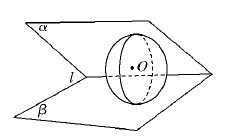
| A. | B.4π | C.12π | D.36π |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 三点处,
三点处, ,
, 到线段
到线段 的距离
的距离 ,
, (参考数据:
(参考数据:  ). 今计划建一个生活垃圾中转站
). 今计划建一个生活垃圾中转站 ,为方便运输,
,为方便运输, 准备建在线段
准备建在线段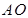 (不含端点)上.
(不含端点)上.
 ,试将
,试将 到三个小区距离的最远者
到三个小区距离的最远者 表示为
表示为 的函数,并求
的函数,并求 的最小值;
的最小值;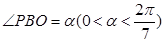 ,试将
,试将 到三个小区的距离之和
到三个小区的距离之和 表示为
表示为 的函数,并确定当
的函数,并确定当 取何值时,可使
取何值时,可使 最小?
最小?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com