
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为直角梯形
为直角梯形![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,![]() 是棱
是棱![]() 上的一点.
上的一点.
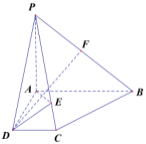
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() ,
,![]() ,且二面角
,且二面角![]() 的正弦值为
的正弦值为![]() ,求
,求![]() 的值.
的值.
科目:高中数学 来源: 题型:
【题目】已知f(x)=|2x+4|+|x-3|.
(1)解关于x的不等式f(x)<8;
(2)对于正实数a,b,函数g(x)=f(x)-3a-4b只有一个零点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年第一期中国青年阅读指数数据显示,从阅读需求的角度,排名前三的阅读领域分别为文学、哲学及社会科学和历史.某学校从文科生和理科生中选取了经常阅读的学生进行了假期阅读内容和阅读时间方面的调查,得到以下数据.
学生所学文理与阅读内容列联表
文学阅读人数 | 非文学阅读人数 | 调查人数 | |
理科生 | 70 | 130 | 200 |
文科生 | 45 | 55 | 100 |
合计 | 115 | 185 | 300 |
(Ⅰ)判断能否有![]() 把握认为学生所学文理与阅读内容有关?
把握认为学生所学文理与阅读内容有关?
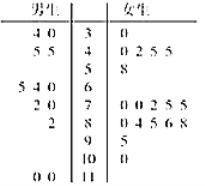
(Ⅱ)从阅读时间大于30分钟的被调查同学中随机选取30名学生,其阅读时间(分钟)整理成如图所示的茎叶图,并绘制日均阅读时间分布表;
其中30名同学的日均阅读时间分布表(单位:分钟)
阅读时间 |
|
|
|
男生人数 | 4 |
| 2 |
女生人数 |
| 10 | 2 |
求出![]() ,
,![]() 的值,并根据日均时间分布表,估计这30名同学日阅读时间的平均值;
的值,并根据日均时间分布表,估计这30名同学日阅读时间的平均值;
(Ⅲ)从(Ⅱ)中日均阅读时间高于90分钟的同学中随机选取2人介绍阅读体会,求这2人性别相同的概率.
参考公式: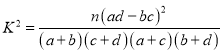 ,其中
,其中![]() .
.
参考数据:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
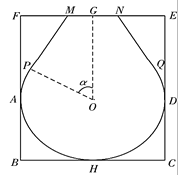
【题目】“金镶玉”是北京奥运会的奖牌设计所采用的式样,喻示中国传统文化中的“金玉良缘”,体现了中国人对奥林匹克精神的礼赞和对运动员的褒奖.它的设计方案,创意十分新颖,突破了以往任何一届奥运会奖牌设计单一材质的传统,又融入了典型的中国文化元素,是中国文化与体育精神完美结合的载体.现有一矩形玉片![]() ,
,![]() 为
为![]() 毫米,
毫米,![]() 为32毫米,
为32毫米,![]() 为
为![]() 的中点.现要开槽镶嵌金丝,将其加工为镶金工艺品,如图,金丝部分为优弧
的中点.现要开槽镶嵌金丝,将其加工为镶金工艺品,如图,金丝部分为优弧![]() 和线段
和线段![]() 其中优弧
其中优弧![]() 所在圆的圆心为
所在圆的圆心为![]() ,圆
,圆![]() 与矩形的边
与矩形的边![]() 分别相切于点
分别相切于点![]() 以及点
以及点![]() 在线段
在线段![]() 上(
上(![]() 在
在![]() 的左侧),
的左侧),![]() 分别于圆
分别于圆![]() 相切于点
相切于点![]() 且
且![]() .若优弧
.若优弧![]() 部分镶嵌的金丝每毫米造价为
部分镶嵌的金丝每毫米造价为![]() 元(
元(![]() ),线段
),线段![]() 部分镶嵌的金丝每毫米造价为
部分镶嵌的金丝每毫米造价为![]() 元.记锐角
元.记锐角![]() 镶嵌金丝的总造价为
镶嵌金丝的总造价为![]() 元.
元.
(1)试表示出关于![]() 的函数
的函数![]() 并写出
并写出![]() 的范围;
的范围;
(2)当镶嵌金丝的总造价最低时,求出四边形![]() 的面积
的面积![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (
(![]() )经过点
)经过点![]() ,离心率为
,离心率为![]() ,
,![]() ,
,![]() 分别为椭圆的左、右焦点.
分别为椭圆的左、右焦点.
(1)求椭圆C的标准方程;
(2)若点![]() (
(![]() )在椭圆C上,求证;直线
)在椭圆C上,求证;直线![]() 与直线
与直线![]() 关于直线l:
关于直线l:![]() 对称.
对称.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为研究![]() 因子对某物种繁殖的影响,某生物研究所开展了系列研究,研究过程中,选取了生长状况相同的三组样本分别标记为
因子对某物种繁殖的影响,某生物研究所开展了系列研究,研究过程中,选取了生长状况相同的三组样本分别标记为![]() 组,
组,![]() 组,
组,![]() 组进行繁殖实验,已知每组均繁殖10个个体,其中
组进行繁殖实验,已知每组均繁殖10个个体,其中![]() 组正常培养,
组正常培养,![]() 组,
组,![]() 组均在食物中添加
组均在食物中添加![]() 因子,一个月后统计存活率,已知
因子,一个月后统计存活率,已知![]() 组存活7个个体,
组存活7个个体,![]() 组存活8个个体,
组存活8个个体,![]() 组存活5个个体,现将这20个存活个体集中,并从中任取3个个体
组存活5个个体,现将这20个存活个体集中,并从中任取3个个体
(1)求抽取的3个存活个体中有来自同一组的概率
(2)记![]() 为所抽取的3个个体中来自
为所抽取的3个个体中来自![]() 组的个体的数量,求
组的个体的数量,求![]() 的分布列和数学期望
的分布列和数学期望
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com