设公司在A和B做广告的时间分别为x分钟和y分钟,总收益为z元,
由题意得
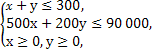
目标函数z=3000x+2000y.
二元一次不等式组等价于
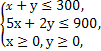
作出二元一次不等式组所表示的平面区域,即可行域,
如图阴影部分.
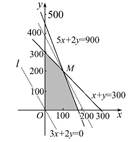
作直线l:3000x+2000y=0,即3x+2y=0,
平移直线l,从图中可知,当直线l过M点时,目标函数取得最大值.
联立
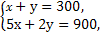
解得
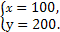
∴点M的坐标为(100,200),
∴z
max=3000×100+2000×200=700000,
即该公司在A电视台做100分钟广告,在B电视台做200分钟广告,公司的收益最大,最大收益是70万元.
【方法技巧】常见的线性规划应用题的类型
(1)给定一定量的人力、物力资源,问怎样运用这些资源,使完成的任务量最大,收益最大.
(2)给定一项任务,问怎样统筹安排,使完成这项任务耗费的人力、物力资源最小.

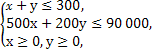
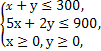

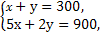
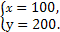


 应用题作业本系列答案
应用题作业本系列答案