
【题目】已知等差数列{an}的公差d≠0,它的前n项和为Sn,若S5=70,且a2,a7,a22成等比数列.
(1)求数列{an}的通项公式;
(2)设数列![]() 的前n项和为Tn,求证:
的前n项和为Tn,求证: ![]() ≤Tn<
≤Tn<![]() .
.
【答案】(1)an=4n+2.(2)见解析
【解析】试题分析:
(1)由题意得到关于首项、公差的方程组,求解方程组可得a1=6,d=4.所以数列{an}的通项公式为an=4n+2(n∈N*).
(2)裂项求和可得![]() ,则
,则![]() ,结合前n项和公式可证得数列{Tn}是递增数列,则Tn≥T1=
,结合前n项和公式可证得数列{Tn}是递增数列,则Tn≥T1=![]() ,据此即可证得题中的结论.
,据此即可证得题中的结论.
试题解析:
(1)因为数列{an}是等差数列,
所以an=a1+(n-1)d,Sn=na1+![]() d.
d.
依题意,有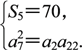
即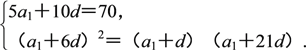
解得a1=6,d=4.
所以数列{an}的通项公式为an=4n+2(n∈N*).
(2)证明:由(1)可得Sn=2n2+4n.
所以![]() =
=![]() =
=![]() =
=![]() (
(![]() -
-![]() ).
).
所以Tn=![]() +
+![]() +
+![]() +…+
+…+![]() +
+![]() =
=![]()
![]() +
+![]()
![]() +
+![]()
![]() +…+
+…+![]() ·
·
![]() +
+![]()
![]() =
=
![]()
![]() =
=![]() -
-![]()
![]() .
.
因为Tn-![]() =-
=-![]()
![]() <0,所以Tn<
<0,所以Tn<![]() .
.
因为Tn+1-Tn=![]()
![]() >0,所以数列{Tn}是递增数列,
>0,所以数列{Tn}是递增数列,
所以Tn≥T1=![]() .所以
.所以![]() ≤Tn<
≤Tn<![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,在三棱锥 ![]() 中,
中, ![]() 底面
底面 ![]() 分别是
分别是 ![]() 的中点,
的中点, ![]() 在
在 ![]() ,且
,且 ![]() .
.
(1)求证: ![]() 平面
平面 ![]() ;
;
(2)在线段 ![]() 上是否存在点
上是否存在点 ![]() ,使二面角
,使二面角 ![]() 的大小为
的大小为 ![]() ?若存在,求出
?若存在,求出 ![]() 的长;
的长;
若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C: ![]() ,点
,点 ![]() 在x轴的正半轴上,过点M的直线
在x轴的正半轴上,过点M的直线 ![]() 与抛物线C相交于A,B两点,O为坐标原点.
与抛物线C相交于A,B两点,O为坐标原点.
(1)若 ![]() ,且直线
,且直线 ![]() 的斜率为1,求以AB为直径的圆的方程;
的斜率为1,求以AB为直径的圆的方程;
(2)是否存在定点M,使得不论直线 ![]() 绕点M如何转动,
绕点M如何转动, ![]() 恒为定值?
恒为定值?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋中有a个黑球和b个白球,随机地每次从中取出一球,每次取后不放回,记事件A为“直到第k次才取到黑球”,其中1≤k≤b;事件B为“第7次取出的球恰好是黑球”,其中1≤k≤b。
(Ⅰ)若a=5,b=3,k=2,求事件A发生的概率;
(Ⅱ)判断事件B发生的概率是否随k取值的变化而变化?并说明理由;
(Ⅲ)比较a=5,b=9时事件A发生的概率与a=5,b=10时事件A发生的概率的大小,并说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 、
、![]() 是两条不同的直线,
是两条不同的直线, ![]() ,
, ![]() ,
, ![]() 是三个不同的平面,给出下列四个命题:
是三个不同的平面,给出下列四个命题:
①若![]() ,
, ![]() ,则
,则![]() ②若
②若![]() ,
, ![]() ,
, ![]() ,则
,则![]()
③若![]() ,
, ![]() ,则
,则![]() ④若
④若![]() ,
, ![]() ,则
,则![]()
其中正确命题的序号是( ).
A. ①和② B. ②和③ C. ③和④ D. ①和④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线过点(3,-2)且与椭圆4x2+9y2=36有相同的焦点.
(I)求双曲线的标准方程.
(II)若点M在双曲线上, ![]() 是双曲线的左、右焦点,且|MF1|+|MF2|=
是双曲线的左、右焦点,且|MF1|+|MF2|=![]() 试判断
试判断![]() 的形状.
的形状.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分14分))
某蔬菜基地种植西红柿,由历年市场行情得知,从二月一日起的300天内,西红柿场售价与上市时间的关系用图一的一条折线表示;西红柿的种植成本与上市时间的关系用图二的抛物线段表示。
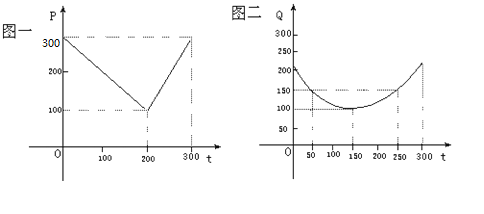
(Ⅰ)写出图一表示的市场售价与时间的函数关系式![]() ;写出图二表示的种植成本与上市时间的函数关系式
;写出图二表示的种植成本与上市时间的函数关系式![]() ;
;
(Ⅱ)假如设定市场售价减去种植成本为纯收益,问何时上市的西红柿纯收益最大?(注:市场售价和种植成本的单位:元/102㎏,时间单位:天)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com