
【题目】已知函数![]() .
.
(1)若![]() 是函数
是函数![]() 的极值点,求
的极值点,求![]() 的单调区间;
的单调区间;
(2)当![]() 时,证明:
时,证明:![]()
【答案】(1)递减区间为(-1,0),递增区间为![]() (2)见解析
(2)见解析
【解析】
(1)根据函数解析式,先求得导函数,由![]() 是函数
是函数![]() 的极值点可求得参数
的极值点可求得参数![]() .求得函数定义域,并根据导函数的符号即可判断单调区间.
.求得函数定义域,并根据导函数的符号即可判断单调区间.
(2)当![]() 时,
时,![]() .代入函数解析式放缩为
.代入函数解析式放缩为![]() ,代入证明的不等式可化为
,代入证明的不等式可化为![]() ,构造函数
,构造函数![]() ,并求得
,并求得![]() ,由函数单调性及零点存在定理可知存在唯一的
,由函数单调性及零点存在定理可知存在唯一的![]() ,使得
,使得![]() 成立,因而求得函数
成立,因而求得函数![]() 的最小值
的最小值![]() ,由对数式变形化简可证明
,由对数式变形化简可证明![]() ,即
,即![]() 成立,原不等式得证.
成立,原不等式得证.
(1)函数![]()
可求得![]() ,则
,则![]()
解得![]()
所以![]() ,定义域为
,定义域为![]()
![]() ,
,
![]() 在
在![]() 单调递增,而
单调递增,而![]() ,
,
∴当![]() 时,
时,![]() ,
,![]() 单调递减,
单调递减,
当![]() 时,
时,![]() ,
,![]() 单调递增,
单调递增,
此时![]() 是函数
是函数![]() 的极小值点,
的极小值点,
![]() 的递减区间为
的递减区间为![]() ,递增区间为
,递增区间为![]()
(2)证明:当![]() 时,
时,![]()
![]() ,
,
因此要证当![]() 时,
时,![]() ,
,
只需证明![]() ,
,
即![]()
令![]() ,
,
则![]() ,
,
![]() 在
在![]() 是单调递增,
是单调递增,
而![]() ,
,
∴存在唯一的![]() ,使得
,使得![]() ,
,
当![]() ,
,![]() 单调递减,当
单调递减,当![]() ,
,![]() 单调递增,
单调递增,
因此当![]() 时,函数
时,函数![]() 取得最小值
取得最小值![]() ,
,
![]() ,
,
![]() ,
,
故![]() ,
,
从而![]() ,即
,即![]() ,结论成立.
,结论成立.


科目:高中数学 来源: 题型:
【题目】每年的寒冷天气都会带热“御寒经济”,以餐饮业为例,当外面太冷时,不少人都会选择叫外卖上门,外卖商家的订单就会增加,下表是某餐饮店从外卖数据中抽取的5天的日平均气温与外卖订单数.
![]()
(Ⅰ)经过数据分析,一天内平均气温![]() 与该店外卖订单数
与该店外卖订单数![]() (份)成线性相关关系,试建立
(份)成线性相关关系,试建立![]() 关于
关于![]() 的回归方程,并预测气温为
的回归方程,并预测气温为![]() 时该店的外卖订单数(结果四舍五入保留整数);
时该店的外卖订单数(结果四舍五入保留整数);
(Ⅱ)天气预报预测未来一周内(七天),有3天日平均气温不高于![]() ,若把这7天的预测数据当成真实数据,则从这7天任意选取2天,求恰有1天外卖订单数不低于160份的概率.
,若把这7天的预测数据当成真实数据,则从这7天任意选取2天,求恰有1天外卖订单数不低于160份的概率.
附注:回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: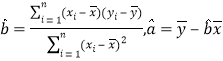 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在①![]() ;②
;②![]() ;③
;③![]() 这三个条件中任选一个,补充在下面问题中的横线上,并解答相应的问题.
这三个条件中任选一个,补充在下面问题中的横线上,并解答相应的问题.
在![]() 中,内角A,B,C的对边分别为a,b,c,且满足________________,
中,内角A,B,C的对边分别为a,b,c,且满足________________,![]()
![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,直线l的参数方程为![]() (t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为
(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为![]() ,直线l与曲线C交于A,B两个不同的点.
,直线l与曲线C交于A,B两个不同的点.
(1)求曲线C的直角坐标方程;
(2)若点P为直线l与x轴的交点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列![]() 是公差为d(
是公差为d(![]() )的等差数列,它的前n项和记为
)的等差数列,它的前n项和记为![]() ,数列
,数列![]() 是公比为q(
是公比为q(![]() )的等比数列,它的前n项和记为
)的等比数列,它的前n项和记为![]() .若
.若![]() ,且存在不小于3的正整数
,且存在不小于3的正整数![]() ,使
,使![]() .
.
(1)若![]() ,求
,求![]() .
.
(2)若![]() 试比较
试比较![]() 与
与![]() 的大小,并说明理由;
的大小,并说明理由;
(3)若![]() ,是否存在整数m,k,使
,是否存在整数m,k,使![]() 若存在,求出m,k的值;若不存在,说明理由.
若存在,求出m,k的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为大力提倡“厉行节约,反对浪费”,衡阳市通过随机询问100名性别不同的居民是否做到“光盘”行动,得到如右列联表及附表:经计算: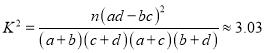 参照附表,得到的正确结论是( )
参照附表,得到的正确结论是( )
做不到“光盘”行动 | 做到“光盘”行动 | |
男 | 45 | 10 |
女 | 30 | 15 |
|
|
|
|
k |
|
|
|
A.在犯错误的概率不超过1%的前提下,认为“该市民能否做到‘光盘’行动与性别有关”
B.在犯错误的概率不超过1%的前提下,认为“该市民能否做到‘光盘’行动与性别无关”
C.有90%以上的把握认为“该市民能否做到‘光盘’行动与性别有关”
D.有90%以上的把握认为“该市民能否做到‘光盘’行动与性别无关”
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com