
ΓΨΧβΡΩΓΩΈΔ–≈ΚλΑϋ «“ΜΩνΩ…“‘ Βœ÷ ’ΖΔΚλΑϋΓΔ≤ι ’Φ«¬ΦΚΆΧαœ÷ΒΡ ÷Μζ”Π”ΟΘ°Ρ≥Άχ¬γ‘Υ”Σ…ΧΕ‘ΦΉΓΔ““ΝΫΗωΤΖ≈ΤΗς5÷÷–ΆΚ≈ΒΡ ÷Μζ‘ΎœύΆ§ΜΖΨ≥œ¬Θ§Ε‘ΥϋΟ««άΒΫΒΡΚλΑϋΗω ΐΫχ––Ά≥ΦΤΘ§ΒΟΒΫ»γ±μ ΐΨίΘΚ
–ΆΚ≈ | Δώ | Δρ | Δσ | Δτ | Δθ |
ΦΉΤΖ≈ΤΘ®ΗωΘ© | 4 | 3 | 8 | 6 | 12 |
““ΤΖ≈ΤΘ®ΗωΘ© | 5 | 7 | 9 | 4 | 3 |
Θ®ΔώΘ©»γΙϊ«άΒΫΚλΑϋΗω ΐ≥§Ιΐ5ΗωΒΡ ÷Μζ–ΆΚ≈ΈΣΓΑ”≈Γ±Θ§Ζώ‘ρΓΑΖ«”≈Γ±Θ§«κΨί¥Υ≈–Εœ «Ζώ”–85%ΒΡΑ―Έ’»œΈΣ«άΒΫΒΡΚλΑϋΗω ΐ”κ ÷ΜζΤΖ≈Τ”–ΙΊΘΩ
Θ®ΔρΘ©»γΙϊ≤ΜΩΦ¬«ΤδΥϋ“ρΥΊΘ§“Σ¥”ΦΉΤΖ≈ΤΒΡ5÷÷–ΆΚ≈÷–―Γ≥ω3÷÷–ΆΚ≈ΒΡ ÷ΜζΫχ––¥σΙφΡΘ–ϊ¥Ϊœζ έΘ°
ΔΌ«σ‘Ύ–ΆΚ≈Δώ±Μ―Γ÷–ΒΡΧθΦΰœ¬Θ§–ΆΚ≈Δρ“≤±Μ―Γ÷–ΒΡΗ≈¬ ΘΜ
ΔΎ“‘X±μ Ψ―Γ÷–ΒΡ ÷Μζ–ΆΚ≈÷–«άΒΫΒΡΚλΑϋ≥§Ιΐ5ΗωΒΡ–ΆΚ≈÷÷ ΐΘ§«σΥφΜζ±δΝΩXΒΡΖ÷≤ΦΝ–ΦΑ ΐ―ßΤΎΆϊEΘ®XΘ©Θ°
œ¬ΟφΝΌΫγ÷Β±μΙ©≤ΈΩΦΘΚ
PΘ®K2Γίk0Θ© | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
≤ΈΩΦΙΪ ΫΘΚK2= ![]() Θ°
Θ°
ΓΨ¥πΑΗΓΩΫβΘΚΘ®ΔώΘ©ΗυΨίΧβ“βΝ–≥ω2ΓΝ2Ν–ΝΣ±μ»γœ¬ΘΚ
ΚλΑϋΗω ΐ ÷ΜζΤΖ≈Τ | ”≈ | Ζ«”≈ | ΚœΦΤ |
ΦΉΤΖ≈ΤΘ®ΗωΘ© | 3 | 2 | 5 |
““ΤΖ≈ΤΘ®ΗωΘ© | 2 | 3 | 5 |
ΚœΦΤ | 5 | 5 | 10 |
![]() Θ§
Θ§
Υυ“‘ΟΜ”–85%ΒΡάμ”…»œΈΣ«άΒΫΚλΑϋΗω ΐ”κ ÷ΜζΤΖ≈Τ”–ΙΊΘ°
Θ®ΔρΘ©ΔΌΝν ¬ΦΰCΈΣΓΑ–ΆΚ≈ I±Μ―Γ÷–Γ±ΘΜ ¬ΦΰDΈΣΓΑ–ΆΚ≈ II±Μ―Γ÷–Γ±Θ§
‘ρ ![]() Θ§
Θ§
Υυ“‘ ![]() Θ°
Θ°
ΔΎΥφΜζ±δΝΩXΒΡΥυ”–Ω…Ρή»Γ÷ΒΈΣ1Θ§2Θ§3Θ§
![]() ΘΜ
ΘΜ
![]() ΘΜ
ΘΜ
![]() Θ°
Θ°
Ι XΒΡΖ÷≤ΦΝ–ΈΣΘΚ
X | 1 | 2 | 3 |
P | | | |
Γύ ΐ―ßΤΎΆϊEΘ®XΘ©Θ§ ![]() Θ°
Θ°
ΓΨΫβΈωΓΩΘ®ΔώΘ©ΗυΨίΧβ“βΝ–≥ω2ΓΝ2Ν–ΝΣ±μΘ§ΗυΨί2ΓΝ2Ν–ΝΣ±μΘ§¥ζ»κ«σΝΌΫγ÷ΒΒΡΙΪ ΫΘ§«σ≥ωΙέ≤β÷ΒΘ§άϊ”ΟΙέ≤β÷ΒΆ§ΝΌΫγ÷Β±μΫχ––±»ΫœΘ§K2=0.4ΘΦ2.706Θ§Ω…ΒΟΒΫΟΜ”–ΉψΙΜΒΡάμ”…»œΈΣ ÷ΜζœΒΆ≥”κΏίΒΟΚλΑϋΉήΫπΕνΒΡΕύ…Ό”–ΙΊΘΜΘ®ΔρΘ©”…Χβ“β«σΒΟXΒΡ»Γ÷Β1Θ§2Θ§3Θ§‘Υ”Ο≈≈Ν–ΉιΚœΒΡ÷Σ ΕΘ§Ω…ΒΟΗςΉ‘ΒΡΗ≈¬ Θ§«σΒΟXΒΡΖ÷≤ΦΝ–Θ§”…ΤΎΆϊΙΪ ΫΦΤΥψΦ¥Ω…ΒΟΒΫΘ®XΘ©Θ°


 Οϊ≈Τ―ß–ΘΖ÷≤ψ÷ή÷ή≤βœΒΝ–¥πΑΗ
Οϊ≈Τ―ß–ΘΖ÷≤ψ÷ή÷ή≤βœΒΝ–¥πΑΗ ΜΤΗ‘ΚΘΒμ»Ϊ≥Χ≈ύ”≈≤β ‘ΨμœΒΝ–¥πΑΗ
ΜΤΗ‘ΚΘΒμ»Ϊ≥Χ≈ύ”≈≤β ‘ΨμœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘Ύ÷±Ϋ«Ήχ±ξœΒxOy÷–Θ§÷±œΏl1ΒΡ≤Έ ΐΖΫ≥ΧΈΣ ![]() Θ§Θ®tΈΣ≤Έ ΐΘ©Θ§÷±œΏl2ΒΡ≤Έ ΐΖΫ≥ΧΈΣ
Θ§Θ®tΈΣ≤Έ ΐΘ©Θ§÷±œΏl2ΒΡ≤Έ ΐΖΫ≥ΧΈΣ  Θ§Θ®mΈΣ≤Έ ΐΘ©Θ°…ηl1”κl2ΒΡΫΜΒψΈΣPΘ§Β±k±δΜ· ±Θ§PΒΡΙλΦΘΈΣ«ζœΏCΘ°
Θ§Θ®mΈΣ≤Έ ΐΘ©Θ°…ηl1”κl2ΒΡΫΜΒψΈΣPΘ§Β±k±δΜ· ±Θ§PΒΡΙλΦΘΈΣ«ζœΏCΘ°
Θ®1Θ©–¥≥ωCΒΡΤ’Ά®ΖΫ≥ΧΘΜ
Θ®2Θ©“‘Ήχ±ξ‘≠ΒψΈΣΦΪΒψΘ§x÷α’ΐΑκ÷αΈΣΦΪ÷αΫ®ΝΔΦΪΉχ±ξœΒΘ§…ηl3ΘΚΠ―Θ®cosΠ»+sinΠ»Θ©©¹ ![]() =0Θ§MΈΣl3”κCΒΡΫΜΒψΘ§«σMΒΡΦΪΨΕΘ°
=0Θ§MΈΣl3”κCΒΡΫΜΒψΘ§«σMΒΡΦΪΨΕΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΒψM(2Θ§2)Θ§N(5Θ§-2)Θ§ΒψP‘Ύx÷α…œΘ§Ζ÷±π«σ¬ζΉψœ¬Ν–ΧθΦΰΒΡΒψPΒΡΉχ±ξ.
(1)ΓœMOP=ΓœOPN(O «Ήχ±ξ‘≠Βψ).
(2)ΓœMPN «÷±Ϋ«.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷Σάβ≥ΛΈΣ1ΒΡ’ΐΖΫΧεABCD-A1B1C1D1÷–Θ§ΒψEΘ§FΘ§MΖ÷±π «ABΘ§ADΘ§AA1ΒΡ÷–ΒψΘ§”÷PΘ§QΖ÷±π‘ΎœΏΕΈA1B1Θ§A1D1…œΘ§«“A1P=A1Q=xΘ§0<x<1Θ§…ηΤΫΟφMEFΓ…ΤΫΟφMPQ=lΘ§‘ρœ¬Ν–Ϋα¬έ÷–≤Μ≥…ΝΔΒΡ «ΓΓ(ΓΓΓΓ)
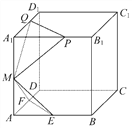
A. lΓΈΤΫΟφABCD
B. lΓΆAC
C. ΤΫΟφMEF”κΤΫΟφMPQ≤Μ¥Ι÷±
D. Β±x±δΜ· ±Θ§l≤Μ «Ε®÷±œΏ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥ΗΏ–Θ¥σ“Μ–¬…ζ÷–ΒΡ6ΟϊΆ§―ߥρΥψ≤ΈΦ”―ß–ΘΉι÷·ΒΡΓΑ―ίΫ≤Ά≈Γ±ΓΔΓΑΦΣΥϊ–≠ΜαΓ±Β»ΈεΗω…γΆ≈Θ§»τΟΩΟϊΆ§―ß±Ί–κ≤ΈΦ”«“÷ΜΡή≤ΈΦ”1Ηω…γΆ≈«“ΟΩΗω…γΆ≈÷ΝΕύΝΫ»Υ≤ΈΦ”Θ§‘ρ’β6Ηω»Υ÷–ΟΜ”–»Υ≤ΈΦ”ΓΑ―ίΫ≤Ά≈Γ±ΒΡ≤ΜΆ§≤ΈΦ”ΖΫΖ® ΐΈΣΘ® Θ©
A.3600
B.1080
C.1440
D.2520
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΡ≥ΦΗΚΈΧεΒΡΗ© ”ΆΦ «»γΆΦΥυ ΨΒΡΨΊ–Έ,’ΐ ”ΆΦ «“ΜΗωΒΉ±Ώ≥ΛΈΣ8ΓΔΗΏΈΣ4ΒΡΒ»―ϋ»ΐΫ«–Έ,≤ύ ”ΆΦ «“ΜΗωΒΉ±Ώ≥ΛΈΣ6ΓΔΗΏΈΣ4ΒΡΒ»―ϋ»ΐΫ«–ΈΘ°

(1)«σΗΟΦΗΚΈΧεΒΡΧεΜΐ![]() ;
;
(2)«σΗΟΦΗΚΈΧεΒΡ±μΟφΜΐ![]() .
.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΥυ ΨΘ§“―÷Σ’ΐΖΫΧεABCDΘ≠A1B1C1D1.
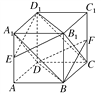
(1)«σ÷ΛΘΚΤΫΟφA1BDΓΈΤΫΟφB1D1C.
(2)»τEΘ§FΖ÷±π «AA1Θ§CC1ΒΡ÷–ΒψΘ§«σ÷ΛΘΚΤΫΟφEB1D1ΓΈΤΫΟφFBD.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘Ύ÷±Ϋ«Ήχ±ξœΒxoy÷–Θ§«ζœΏC1ΘΚ ![]() Θ®tΈΣ≤Έ ΐΘ§tΓΌ0Θ©Θ§Τδ÷–0ΓήΠΝΘΦΠ–Θ§‘Ύ“‘OΈΣΦΪΒψΘ§x÷α’ΐΑκ÷αΈΣΦΪ÷αΒΡΦΪΉχ±ξœΒ÷–Θ§«ζœΏC2ΘΚΠ―=2sinΠ»Θ§«ζœΏC3ΘΚΠ―=2
Θ®tΈΣ≤Έ ΐΘ§tΓΌ0Θ©Θ§Τδ÷–0ΓήΠΝΘΦΠ–Θ§‘Ύ“‘OΈΣΦΪΒψΘ§x÷α’ΐΑκ÷αΈΣΦΪ÷αΒΡΦΪΉχ±ξœΒ÷–Θ§«ζœΏC2ΘΚΠ―=2sinΠ»Θ§«ζœΏC3ΘΚΠ―=2 ![]() cosΠ»Θ° Θ®ΔώΘ©«σC2”κC3ΫΜΒψΒΡ÷±Ϋ«Ήχ±ξΘΜ
cosΠ»Θ° Θ®ΔώΘ©«σC2”κC3ΫΜΒψΒΡ÷±Ϋ«Ήχ±ξΘΜ
Θ®ΔρΘ©»τC2”κC1œύΫΜ”ΎΒψAΘ§C3”κC1œύΫΜ”ΎΒψBΘ§«σ|AB|ΒΡΉν¥σ÷ΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΈΣΝΥ―–ΨΩ“Μ÷÷άΞ≥φΒΡ≤ζ¬― ΐyΚΆΈ¬Ε»x «Ζώ”–ΙΊΘ§œ÷ ’Φ·ΝΥ7ΉιΙέ≤β ΐΨίΝ–”Ύœ¬±μ÷–Θ§≤ΔΉω≥ωΝΥ…ΔΒψΆΦΘ§ΖΔœ÷―υ±ΨΒψ≤ΔΟΜ”–Ζ÷≤Φ‘ΎΡ≥Ηω¥χΉ¥«χ”ρΡΎΘ§ΝΫΗω±δΝΩ≤Δ≤Μ≥ œ÷œΏ–‘œύΙΊΙΊœΒΘ§œ÷Ζ÷±π”ΟΡΘ–ΆΔΌ ![]() ”κΡΘ–ΆΘΜΔΎ
”κΡΘ–ΆΘΜΔΎ ![]() ΉςΈΣ≤ζ¬― ΐyΚΆΈ¬Ε»xΒΡΜΊΙιΖΫ≥Χά¥Ϋ®ΝΔΝΫΗω±δΝΩ÷°ΦδΒΡΙΊœΒΘ°
ΉςΈΣ≤ζ¬― ΐyΚΆΈ¬Ε»xΒΡΜΊΙιΖΫ≥Χά¥Ϋ®ΝΔΝΫΗω±δΝΩ÷°ΦδΒΡΙΊœΒΘ°
Έ¬Ε»x/ΓψC | 20 | 22 | 24 | 26 | 28 | 30 | 32 |
≤ζ¬― ΐy/Ηω | 6 | 10 | 21 | 24 | 64 | 113 | 322 |
t=x2 | 400 | 484 | 576 | 676 | 784 | 900 | 1024 |
z=lny | 1.79 | 2.30 | 3.04 | 3.18 | 4.16 | 4.73 | 5.77 |
| | | |
26 | 692 | 80 | 3.57 |
| | | |
1157.54 | 0.43 | 0.32 | 0.00012 |
Τδ÷– ![]() Θ§
Θ§ ![]() Θ§zi=lnyi Θ§
Θ§zi=lnyi Θ§ ![]() Θ§
Θ§
ΗΫΘΚΕ‘”Ύ“ΜΉι ΐΨίΘ®ΠΧ1 Θ§ ΠΆ1Θ©Θ§Θ®ΠΧ2 Θ§ ΠΆ2Θ©Θ§Θ®ΠΧn Θ§ ΠΆnΘ©Θ§ΤδΜΊΙι÷±œΏv=Π¬ΠΧ+ΠΝΒΡ–±¬ ΚΆΫΊΨύΒΡΉν–ΓΕΰ≥ΥΙάΦΤΖ÷±πΈΣΘΚ  Θ§
Θ§ ![]()
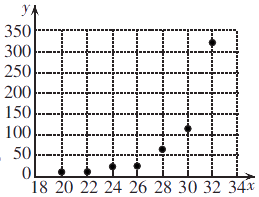
Θ®1Θ©ΗυΨί±μ÷– ΐΨίΘ§Ζ÷±πΫ®ΝΔΝΫΗωΡΘ–Άœ¬yΙΊ”ΎxΒΡΜΊΙιΖΫ≥ΧΘΜ≤Δ‘ΎΝΫΗωΡΘ–Άœ¬Ζ÷±πΙάΦΤΈ¬Ε»ΈΣ30ΓψC ±ΒΡ≤ζ¬― ΐΘ°Θ®C1 Θ§ C2 Θ§ C3 Θ§ C4”κΙάΦΤ÷ΒΨυΨΪ»ΖΒΫ–Γ ΐΒψΚσΝΫΈΜΘ©Θ®≤ΈΩΦ ΐΨίΘΚe4.65Γ÷104.58Θ§e4.85Γ÷127.74Θ§e5.05Γ÷156.02Θ©
Θ®2Θ©»τΡΘ–ΆΔΌΓΔΔΎΒΡœύΙΊ÷Η ΐΦΤΥψΖ÷±πΈΣ ![]() Θ°Θ§«κΗυΨίœύΙΊ÷Η ΐ≈–ΕœΡΡΗωΡΘ–ΆΒΡΡβΚœ–ßΙϊΗϋΚΟΘ°
Θ°Θ§«κΗυΨίœύΙΊ÷Η ΐ≈–ΕœΡΡΗωΡΘ–ΆΒΡΡβΚœ–ßΙϊΗϋΚΟΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΑΌΕ»÷¬–≈ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com