
【题目】2019年9月28日中国女排在世界杯第10轮比赛中,以![]() 的比分战胜塞尔维亚女排,从而在本次女排世界杯中取得10连胜,提前一轮卫冕世界杯冠军.世界杯是单循环赛制,中国女排要和11个对手轮番对决,比赛中以
的比分战胜塞尔维亚女排,从而在本次女排世界杯中取得10连胜,提前一轮卫冕世界杯冠军.世界杯是单循环赛制,中国女排要和11个对手轮番对决,比赛中以![]() 或
或![]() 取胜的球队积3分,负队积0分,而在比赛中以
取胜的球队积3分,负队积0分,而在比赛中以![]() 取胜的球队积2分,负队积1分,通过最终的总积分来决定最后的名次归属.
取胜的球队积2分,负队积1分,通过最终的总积分来决定最后的名次归属.
下某网站上整理了2003年以来中国队与世界女排强队的50场比赛胜负情况如下表.
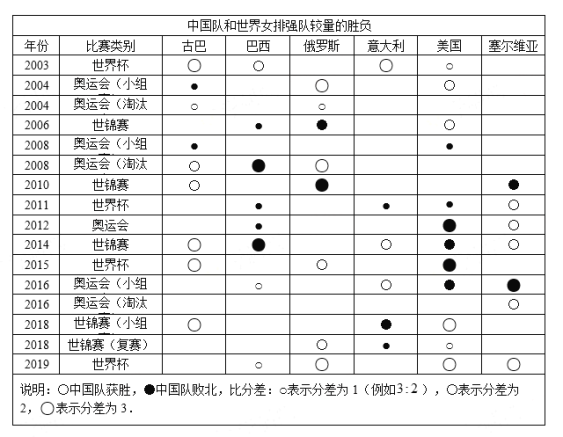
(1)现从中国队与美国女排及俄罗斯女排的比赛视频中各调取1场比赛进行观看,求至少有一场是中国队以3:0获胜的比赛的概率;
(2)若根据表中数据进行推断:
①求中国队与巴西队比赛获得的积分期望;
②预测中国队、巴西、俄罗斯、美国这四支强队进行单循环赛时中国队获得总积分的期望.
【答案】(1)![]() ;(2)①
;(2)①![]() ;②
;②![]() .
.
【解析】
(1)根据表中数据可计算基本事件的总数和随机事件中含有的基本事件的总数,从而可得所求的概率.
(2)根据表中数据可得中国队与巴西队比赛结果为:得3分的次数为1次,得2分的次数为2次, 得1分的次数为3次,得0分的次数为1次,计算出相应的概率(频率)可得随机变量![]() 的分布列.同理可得与俄罗斯比赛获得积分的随机变量
的分布列.同理可得与俄罗斯比赛获得积分的随机变量![]() 、与美国比赛获得积分的随机变量
、与美国比赛获得积分的随机变量![]() 的分布列,再计算出各自的数学期望后可得总积分的期望.
的分布列,再计算出各自的数学期望后可得总积分的期望.
解:(1)记至少有一场是中国队3∶0获胜为事件![]() ,
,
则![]() .
.
(2)①获得的积分随机变量![]() 可能为0,1,2,3,
可能为0,1,2,3,
则由表格可知:![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以随机变量![]() 的分布列为
的分布列为
| 0 | 1 | 2 | 3 |
|
|
|
|
|
所以期望为![]() .
.
②设与俄罗斯比赛获得积分的随机变量为![]() ,则分布列为
,则分布列为
| 0 | 2 | 3 |
|
|
|
|
所以期望为![]() .
.
设与美国比赛获得积分的随机变量为![]() ,则分布列为
,则分布列为
| 0 | 1 | 2 | 3 |
|
|
|
|
|
所以期望为![]() ,
,
所以总积分的期望为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数![]() 为奇函数,
为奇函数,![]() ,其中
,其中![]() .
.
(1)若函数![]() 的图像过点
的图像过点![]() ,求实数
,求实数![]() 和
和![]() 的值;
的值;
(2)若![]() ,试判断函数
,试判断函数![]() 在
在![]() 上的单调性并证明;
上的单调性并证明;
(3)设函数 ,若对每一个不小于3的实数
,若对每一个不小于3的实数![]() ,都恰有一个小于3的实数
,都恰有一个小于3的实数![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数学中有许多形状优美、寓意美好的曲线,曲线C:![]() 就是其中之一(如图).给出下列三个结论:
就是其中之一(如图).给出下列三个结论:

①曲线C恰好经过6个整点(即横、纵坐标均为整数的点);
②曲线C上任意一点到原点的距离都不超过![]() ;
;
③曲线C所围成的“心形”区域的面积小于3.
其中,所有正确结论的序号是
A. ①B. ②C. ①②D. ①②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的方程为
的方程为![]() ,圆
,圆![]() 与
与![]() 轴相切于点
轴相切于点![]() ,与
,与![]() 轴正半轴相交于
轴正半轴相交于![]() 、
、![]() 两点,且
两点,且![]() ,如图1.
,如图1.
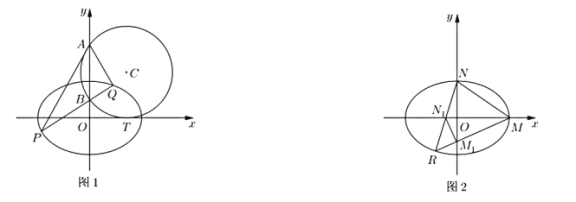
(1)求圆![]() 的方程;
的方程;
(2)如图1,过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 、
、![]() 两点,求证:射线
两点,求证:射线![]() 平分
平分![]() ;
;
(3)如图2所示,点![]() 、
、![]() 是椭圆
是椭圆![]() 的两个顶点,且第三象限的动点
的两个顶点,且第三象限的动点![]() 在椭圆
在椭圆![]() 上,若直线
上,若直线![]() 与
与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,试问:四边形
,试问:四边形![]() 的面积是否为定值?若是,请求出这个定值,若不是,请说明理由.
的面积是否为定值?若是,请求出这个定值,若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是菱形,点
是菱形,点![]() 在线段
在线段![]() 上,
上,![]() ,
,![]() 是线段
是线段![]() 的中点,且三棱锥
的中点,且三棱锥![]() 的体积是四棱锥
的体积是四棱锥![]() 体积的
体积的![]() .
.
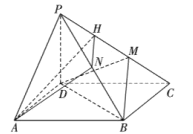
(1)若![]() 是
是![]() 的中点,证明:平面
的中点,证明:平面![]() 平面
平面![]() ;
;
(2)若![]() 平面
平面![]() ,求二面角
,求二面角![]() 的正弦值.
的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com