练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知直线的极坐标方程为，曲线的参数方程为（为参数）.

    （1）求直线的直角坐标方程和曲线的普通方程；

    （2）若过且与直线垂直的直线与曲线相交于、两点，求.

    【答案】（1），；（2）

    【解析】

    (1)根据极坐标与直角坐标方程的转化,参数方程与普通方程的转化即可得直线的直角坐标方程和曲线的普通方程;

    (2)根据直线与直线垂直且过,可得直线的参数方程.将直线的参数方程与曲线联立,结合韦达定理及参数方程的几何意义即可求得.

    (1)由直线极坐标方程为,即,

    根据极坐标与直角坐标的互化公式,可得直线直角坐标方程：,

    由曲线的参数方程为（为参数）,则,

    整理得椭圆的普通方程为.

    (2)由已知直线与垂直,所以直线的倾斜角为,

    直线的参数方程为,即（为参数）,

    把直线的参数方程代入

    化简得

    设,是上述方程的两个实根,则有

    又直线过点

    故由上式及的几何意义得

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知椭圆与直线有且只有一个交点，点P为椭圆C上任一点，，.若的最小值为.

    （1）求椭圆C的标准方程；

    （2）设直线与椭圆C交于不同两点A，B，点O为坐标原点，且，当的面积S最大时，求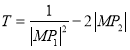的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】“绿水青山就是金山银山”的生态文明发展理念已经深入人心,这将推动新能源汽车产业的迅速发展.下表是近几年我国某地区新能源乘用车的年销售量与年份的统计表：

    年份

    2014

    2015

    2016

    2017

    2018

    销量（万台）

    8

    10

    13

    25

    24

    某机构调查了该地区30位购车车主的性别与购车种类情况，得到的部分数据如下表所示：

    购置传统燃油车

    购置新能源车

    总计

    男性车主

    6

    24

    女性车主

    2

    总计

    30

    （1）求新能源乘用车的销量关于年份的线性相关系数，并判断与是否线性相关；

    （2）请将上述列联表补充完整，并判断是否有的把握认为购车车主是否购置新能源乘用车与性别有关；

    （3）若以这30名购车车主中购置新能源乘用车的车主性别比例作为该地区购置新能源乘用车的车主性别比例,从该地区购置新能源乘用车的车主中随机选取50人,记选到女性车主的人数为X,求X的数学期望与方差.

    参考公式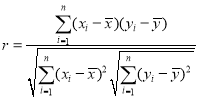：，，其中.，若，则可判断与线性相关.

    附表：

    0．10

    0.05

    0.025

    0.010

    0.001

    2.706

    3.841

    5.024

    6.635

    10.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数（其中）.

    （1）讨论函数的极值；

    （2）对任意，恒成立，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆C：（）的焦距为4，其短轴的两个端点与长轴的一个端点构成正三角形.

    （1）求椭圆C的标准方程；

    （2）设F为椭圆C的左焦点，T为直线上任意一点，过F作TF的垂线交椭圆C于点P，Q.

    （i）证明：OT平分线段PQ（其中O为坐标原点）；

    （ii）当最小时，求点T的坐标.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知定义在上的函数的图像是一条连续不断的曲线，且在任意区间上都不是常值函数.设，其中分点将区间任意划分成个小区间，记，称为关于区间的阶划分“落差总和”.

    当取得最大值且取得最小值时，称存在“最佳划分”.

    (1)已知，求的最大值；

    (2)已知，求证：在上存在“最佳划分”的充要条件是在上单调递增.

    (3)若是偶函数且存在“最佳划分”，求证：是偶数，且.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）讨论函数的单调性；

    （2）对任意的，，，恒有，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知动点P到直线的距离与到点的距离之比为.

    （1）求动点P的轨迹；

    （2）直线与曲线交于不同的两点A,B(A,B在轴的上方)：

    ①当A为椭圆与轴的正半轴的交点时，求直线的方程；

    ②对于动直线，是否存在一个定点，无论如何变化，直线总经过此定点？若存在，求出该定点的坐标；若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】“公平正义”是社会主义和谐社会的重要特征，是社会主义法治理念的价值追求.“考试”作为一种公平公正选拔人才的有效途径，正被广泛采用.每次考试过后，考生最关心的问题是:自己的考试名次是多少？自已能否被录取?能获得什么样的职位？

    某单位准备通过考试(按照高分优先录取的原则)录用名，其中个高薪职位和个普薪职位.实际报名人数为名，考试满分为分. 考试后对部分考生考试成绩进行抽样分析，得到频率分布直方图如下：

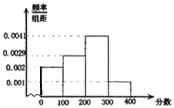
    试结合此频率分布直方图估计：

    (1)此次考试的中位数是多少分（保留为整数）？

    (2)若考生甲的成绩为280分，能否被录取?若能被录取，能否获得高薪职位？(分数精确到个位，概率精确到千分位)

    查看答案和解析>>

    同步练习册答案