
请思考如何利用导数进行求和.
1.Sn=1+2x+3x2+…+nxn-1(x≠0,n∈N*);
2.Sn=![]() +…+n
+…+n![]() (n∈N*).
(n∈N*).
|
导思:1.一般很容易想到通过错位相减的方法及构造二项式定理的方法来解决,转换思维角度.由求导公式(xn)=nxn-1可联想到它们是另外一个和式的导数,因此可转化求和.利用导数运算,可使问题解法更加简捷. 2.通过对数列的通项进行联想,合理运用了逆向思维的方法,从而激发了思维的灵活性,使数列的求和问题得到解决,其关键是抓住了数列通项的形式结构,这也有助于培养善于联想的好习惯. 探究:1.当x=1时,Sn=1+2+3+…+n= (x+x2+x3+…+xn 即Sn=1+2x+3x2+…+nxn-1= 2.(1+x)n=1+ 令x=1,得n·2n-1= 即Sn= |


科目:高中数学 来源:2013届辽宁省高二下学期期中考试文科数学试卷(解析版) 题型:解答题
已知函数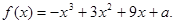
(Ⅰ)求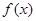 的单调减区间;
的单调减区间;
(Ⅱ)若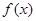 在区间[-2,2].上的最大值为20,求它在该区间上的最小值.
在区间[-2,2].上的最大值为20,求它在该区间上的最小值.
【解析】(1)求导令导数小于零.
(2)利用导数列表求极值,最值即可.
查看答案和解析>>
科目:高中数学 来源:2013届四川省高二下学期期中考试理科数学试卷(解析版) 题型:解答题
已知函数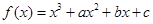 ,曲线
,曲线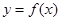 在点
在点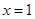 处的切线为
处的切线为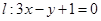 ,若
,若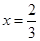 时,
时,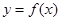 有极值.
有极值.
(1)求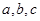 的值;
的值;
(2)求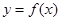 在
在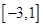 上的最大值和最小值.
上的最大值和最小值.
【解析】(1)根据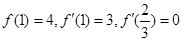 可建立关于a,b,c的三个方程,解方程组即可.
可建立关于a,b,c的三个方程,解方程组即可.
(2)在(1)的基础上,利用导数列表求极值,最值即可.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com