
【题目】下列命题为真命题的个数是( )(其中![]() ,
,![]() 为无理数)
为无理数)
①![]() ;②
;②![]() ;③
;③![]() .
.
A.0B.1C.2D.3
科目:高中数学 来源: 题型:
【题目】已知抛物线E:y2=2px(p>0),焦点F到准线的距离为3,抛物线E上的两个动点A(x1,y1)和B(x2,y2),其中x1≠x2且x1+x2=4.线段AB的垂直平分线与x轴交于点 C.
(1)求抛物线E的方程;
(2)求△ABC面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
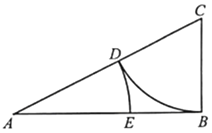
【题目】古希腊雅典学派算学家欧道克萨斯提出了“黄金分割”的理论,利用尺规作图可画出己知线段的黄金分割点,具体方法如下:(l)取线段AB=2,过点B作AB的垂线,并用圆规在垂线上截取BC=![]() AB,连接AC;(2)以C为圆心,BC为半径画弧,交AC于点D;(3)以A为圆心,以AD为半径画弧,交AB于点E.则点E即为线段AB的黄金分割点.若在线段AB上随机取一点F,则使得BE≤AF≤AE的概率约为( )(参考数据:
AB,连接AC;(2)以C为圆心,BC为半径画弧,交AC于点D;(3)以A为圆心,以AD为半径画弧,交AB于点E.则点E即为线段AB的黄金分割点.若在线段AB上随机取一点F,则使得BE≤AF≤AE的概率约为( )(参考数据:![]() 2.236)
2.236)
A. 0.236B. 0.382C. 0.472D. 0.618
查看答案和解析>>
科目:高中数学 来源: 题型:
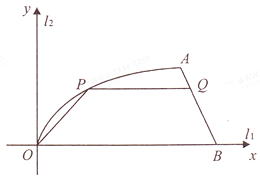
【题目】如图,某小区内有两条互相垂直的道路![]() 与
与![]() ,平面直角坐标系
,平面直角坐标系![]() 的第一象限有一块空地
的第一象限有一块空地![]() ,其边界
,其边界![]() 是函数
是函数![]() 的图象,前一段曲线
的图象,前一段曲线![]() 是函数
是函数![]() 图象的一部分,后一段
图象的一部分,后一段![]() 是一条线段.测得
是一条线段.测得![]() 到
到![]() 的距离为8米,到
的距离为8米,到![]() 的距离为16米,
的距离为16米,![]() 长为20米.
长为20米.
(1)求函数![]() 的解析式;
的解析式;
(2)现要在此地建一个社区活动中心,平面图为梯形![]() (其中
(其中![]() ,
,![]() 为两底边),问:梯形的高为多少米时,该社区活动中心的占地面积最大,并求出最大面积.
为两底边),问:梯形的高为多少米时,该社区活动中心的占地面积最大,并求出最大面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某网店经销某商品,为了解该商品的月销量y(单位:千件)与售价x(单位:元/件)之间的关系,收集5组数据进行了初步处理,得到如下数表:
x | 5 | 6 | 7 | 8 | 9 |
y | 8 | 6 | 4.5 | 3.5 | 3 |
(1)统计学中用相关系数r来衡量两个变量之间线性相关关系的强弱,若![]() ,则认为相关性很强;若
,则认为相关性很强;若![]() ,则认为相关性一般;若
,则认为相关性一般;若![]() ,则认为相关性较弱.请根据上表数据计算y与x之间相关系数r,并说明y与x之间的线性相关关系的强弱(精确到0.01);
,则认为相关性较弱.请根据上表数据计算y与x之间相关系数r,并说明y与x之间的线性相关关系的强弱(精确到0.01);
(2)求y关于x的线性回归方程;
(3)根据(2)中的线性回归方程,应将售价x定为多少,可获取最大的月销售金额?(月销售金额=月销售量×当月售价)
附注:
参考数据:![]() ,
,
参考公式:相关系数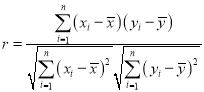 ,
,
线性回归方程![]() ,
, ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】德国著名数学家狄利克雷(Dirichlet,1805~1859)在数学领域成就显著.19世纪,狄利克雷定义了一个“奇怪的函数” 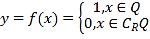 其中R为实数集,Q为有理数集.则关于函数
其中R为实数集,Q为有理数集.则关于函数![]() 有如下四个命题,正确的为( )
有如下四个命题,正确的为( )
A.函数![]() 是偶函数
是偶函数
B.![]() ,
,![]() ,
,![]() 恒成立
恒成立
C.任取一个不为零的有理数T,![]() 对任意的
对任意的![]() 恒成立
恒成立
D.不存在三个点![]() ,
,![]() ,
,![]() ,使得
,使得![]() 为等腰直角三角形
为等腰直角三角形
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】李克强总理在2018年政府工作报告指出,要加快建设创新型国家,把握世界新一轮科技革命和产业变革大势,深入实施创新驱动发展战略,不断增强经济创新力和竞争力.某手机生产企业积极响应政府号召,大力研发新产品,争创世界名牌.为了对研发的一批最新款手机进行合理定价,将该款手机按事先拟定的价格进行试销,得到一组销售数据![]() ,如表所示:
,如表所示:
单价 |
|
|
|
|
|
|
销量 |
|
|
|
|
|
|
已知![]() .
.
(1)若变量![]() 具有线性相关关系,求产品销量
具有线性相关关系,求产品销量![]() (百件)关于试销单价
(百件)关于试销单价![]() (千元)的线性回归方程
(千元)的线性回归方程![]() ;
;
(2)用(1)中所求的线性回归方程得到与![]() 对应的产品销量的估计值
对应的产品销量的估计值![]() .当销售数据
.当销售数据![]() 对应的残差的绝对值
对应的残差的绝对值![]() 时,则将销售数据
时,则将销售数据![]() 称为一个“好数据”.现从
称为一个“好数据”.现从![]() 个销售数据中任取
个销售数据中任取![]() 个子,求“好数据”个数
个子,求“好数据”个数![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
(参考公式:线性回归方程中![]() 的估计值分别为
的估计值分别为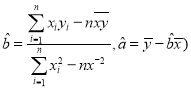 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com