
【题目】为推行“新课堂”教学法, 某化学老师分别用传统教学和“新课堂”两种不同的教学方式, 在甲、乙两个平行班进行教学实验, 为了解教学效果, 期中考试后, 分别从两个班级中各随机抽取20名学生的成绩进行统计, 作出的茎叶图如下图, 记成绩不低于70分者为“成绩优良”.
(1) 分别计算甲、乙两班20个样本中, 化学成绩前十的平均分, 并据此判断哪种教学方式的教学效果更佳;
甲班 | 乙班 | 总计 | |
成绩优良 | |||
成绩不优良 | |||
总 计 |
(2)由以上统计数据填写下面2×2列联表,是否有95%的把握认为“成绩优良与教学方式关”?
| 0.05 | 0.010 |
| 3.841 | 6.635 |
![]()
【答案】(1) ![]() ,
,![]() ,使用“高效教学法”的乙班教学效果更佳.
,使用“高效教学法”的乙班教学效果更佳.
(2) 有![]() 的把握认为“成绩优良”与“教学方式”有关.
的把握认为“成绩优良”与“教学方式”有关.
【解析】分析:(1)先求出甲班、乙班的平均分,然后再作出判断.(2)根据列联表中的数据求出![]() ,再结合临界值表得到结论.
,再结合临界值表得到结论.
详解:(1)甲班化学成绩前10名学生的平均分为
![]()
乙班化学成绩前10名学生的平均分为
![]()
由于![]() ,
,
所以可判断使用“高效教学法”的乙班教学效果更佳.
甲班 | 乙班 | 总计 | |
成绩优良 | 10 | 16 | 26 |
成绩不优良 | 10 | 4 | 14 |
总 计 | 20 | 20 | 40 |
(2)根据茎叶图中的数据,列出列联表如下:
由表中的数据可得![]() ,
,
所以能在犯错误的概率不超过0.05的前提下,即有![]() 的把握认为“成绩优良”与“教学方式”有关.
的把握认为“成绩优良”与“教学方式”有关.


科目:高中数学 来源: 题型:
【题目】如果某地的财政收入![]() 与支出
与支出![]() 满足线性回归方程
满足线性回归方程![]() (单位:亿元),其中
(单位:亿元),其中![]() ,如果今年该地区财政收入10亿元,则年支出预计不会超过( )
,如果今年该地区财政收入10亿元,则年支出预计不会超过( )
A. 10.5亿 B. 10亿 C. 9.5亿 D. 9亿
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知首项为 ![]() 的等比数列{an}不是递减数列,其前n项和为Sn(n∈N*),且S3+a3 , S5+a5 , S4+a4成等差数列.
的等比数列{an}不是递减数列,其前n项和为Sn(n∈N*),且S3+a3 , S5+a5 , S4+a4成等差数列.
(1)求数列{an}的通项公式;
(2)设 ![]() ,求数列{Tn}的最大项的值与最小项的值.
,求数列{Tn}的最大项的值与最小项的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】节日前夕,小李在家门前的树上挂了两串彩灯,这两串彩灯的第一次闪亮相互独立,且都在通电后的4秒内任一时刻等可能发生,然后每串彩灯以4秒为间隔闪亮,那么这两串彩灯同时通电后,它们第一次闪亮的时候相差不超过2秒的概率是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了展示中华汉字的无穷魅力,传递传统文化,提高学习热情,某校开展《中国汉字听写大会》的活动.为响应学校号召,2(9)班组建了兴趣班,根据甲、乙两人近期8次成绩画出茎叶图,如图所示,甲的成绩中有一个数的个位数字模糊,在茎叶图中用![]() 表示.(把频率当作概率).
表示.(把频率当作概率).
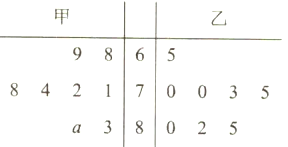
(1)假设![]() ,现要从甲、乙两人中选派一人参加比赛,从统计学的角度,你认为派哪位学生参加比较合适?
,现要从甲、乙两人中选派一人参加比赛,从统计学的角度,你认为派哪位学生参加比较合适?
(2)假设数字![]() 的取值是随机的,求乙的平均分高于甲的平均分的概率.
的取值是随机的,求乙的平均分高于甲的平均分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,侧棱AA1⊥底面ABC,AB=AC=2AA1 , ∠BAC=120°,D,D1分别是线段BC,B1C1的中点,P是线段AD的中点. 
(1)在平面ABC内,试做出过点P与平面A1BC平行的直线l,说明理由,并证明直线l⊥平面ADD1A1;
(2)设(1)中的直线l交AB于点M,交AC于点N,求二面角A﹣A1M﹣N的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l1:x-2y+3=0与直线l2:2x+3y-8=0的交点为M,
(1)求过点M且到点P(0,4)的距离为2的直线l的方程;
(2)求过点M且与直线l3:x+3y+1=0平行的直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一个口袋有![]() 个白球,
个白球,![]() 个黑球,这些球除颜色外全部相同,现将口袋中的球随机逐个取出,并依次放入编号为
个黑球,这些球除颜色外全部相同,现将口袋中的球随机逐个取出,并依次放入编号为![]() ,
,![]() ,
,![]() ,
,![]() 的抽屉内.
的抽屉内.
(1)求编号为![]() 的抽屉内放黑球的概率;
的抽屉内放黑球的概率;
(2)口袋中的球放入抽屉后,随机取出两个抽屉中的球,求取出的两个球是一黑一白的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com