
【题目】已知椭圆![]() 的左、右焦点为别为
的左、右焦点为别为![]() 、
、![]() ,且过点
,且过点![]() 和
和![]() .
.
(1)求椭圆的标准方程;
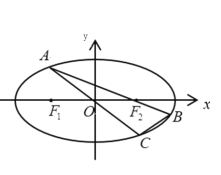
(2)如图,点![]() 为椭圆上一动点(非长轴端点),
为椭圆上一动点(非长轴端点),![]() 的延长线与椭圆交于点
的延长线与椭圆交于点![]() ,
,![]() 的延长线与椭圆交于点
的延长线与椭圆交于点![]() ,求
,求![]() 面积的最大值.
面积的最大值.
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:高中数学 来源: 题型:
【题目】定义区间(m,n),![]() ,
,![]() ,
,![]() 的长度均为
的长度均为![]() ,其中
,其中![]() .
.
(1)若关于x的不等式![]() 的解集构成的区间的长度为
的解集构成的区间的长度为![]() ,求实数a的值;
,求实数a的值;
(2)求关于x的不等式![]() 的解集构成的区间的长度的取值范围;
的解集构成的区间的长度的取值范围;
(3)已知关于x的不等式组 的解集构成的各区间长度和为5,求实数t的取值范围.
的解集构成的各区间长度和为5,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x),g(x)满足关系g(x)=f(x)f(x+α),其中α是常数.
(1)设f(x)=cosx+sinx,![]() ,求g(x)的解析式;
,求g(x)的解析式;
(2)设计一个函数f(x)及一个α的值,使得![]() ;
;
(3)当f(x)=|sinx|+cosx,![]() 时,存在x1,x2∈R,对任意x∈R,g(x1)≤g(x)≤g(x2)恒成立,求|x1-x2|的最小值.
时,存在x1,x2∈R,对任意x∈R,g(x1)≤g(x)≤g(x2)恒成立,求|x1-x2|的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某次测量中得到的A样本数据如下:82,84,84,86,86,86,88,88,88,88.若B样本数据恰好是A样本数据都加2后所得数据,则A,B两样本的下列数字特征对应相同的是
A. 众数 B. 平均数 C. 中位数 D. 标准差
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商品销售价格和销售量与销售天数有关,第x天![]() 的销售价格
的销售价格![]() (元/百斤),第x天
(元/百斤),第x天![]() 的销售量
的销售量![]() (百斤)(a为常数),且第7天销售该商品的销售收入为2009元.
(百斤)(a为常数),且第7天销售该商品的销售收入为2009元.
(1)求第10天销售该商品的销售收入是多少?
(2)这20天中,哪一天的销售收入最大?为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数![]() ,
,![]() 且
且![]() 的定义域为
的定义域为![]() ,
,![]() .
.
(1)求实数![]() 的值,使函数
的值,使函数![]() 为奇函数;
为奇函数;
(2)在(1)的条件下,令![]() ,求使方程
,求使方程![]() ,
,![]() 有解的实数
有解的实数![]() 的取值范围;
的取值范围;
(3)在(1)的条件下,不等式![]() 对于任意的
对于任意的![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以直角坐标系的原点为极点,以
为参数),以直角坐标系的原点为极点,以![]() 轴的正半轴为极轴建立极坐标系,已知直线
轴的正半轴为极轴建立极坐标系,已知直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程;
的普通方程;
(2)若![]() 与曲线
与曲线![]() 相切,且
相切,且![]() 与坐标轴交于
与坐标轴交于![]() 两点,求以
两点,求以![]() 为直径的圆的极坐标方程.
为直径的圆的极坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以平面直角坐标系的原点为极点,![]() 轴的正半轴为极轴,建立极坐标系,已知直线
轴的正半轴为极轴,建立极坐标系,已知直线![]() 的参数方程是
的参数方程是 (m>0,t为参数),曲线
(m>0,t为参数),曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与曲线
,与曲线![]() 交于点
交于点![]() ,且
,且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了研究学生的数学核心素养与抽象能力(指标![]() )、推理能力(指标
)、推理能力(指标![]() )、建模能力(指标
)、建模能力(指标![]() )的相关性,将它们各自量化为1、2、3三个等级,再用综合指标
)的相关性,将它们各自量化为1、2、3三个等级,再用综合指标![]() 的值评定学生的数学核心素养,若
的值评定学生的数学核心素养,若![]() ,则数学核心素养为一级;若
,则数学核心素养为一级;若![]() ,则数学核心素养为二级;若
,则数学核心素养为二级;若![]() ,则数学核心素养为三级,为了了解某校学生的数学核心素养,调查人员随机访问了某校10名学生,得到如下数据:
,则数学核心素养为三级,为了了解某校学生的数学核心素养,调查人员随机访问了某校10名学生,得到如下数据:
学生编号 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)在这10名学生中任取两人,求这两人的建模能力指标相同条件下综合指标值也相同的概率;
(2)在这10名学生中任取三人,其中数学核心素养等级是一级的学生人数记为![]() ,求随机变量
,求随机变量![]() 的分布列及其数学期望.
的分布列及其数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com