
【题目】如图,椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]()
![]() 轴,直线
轴,直线![]() 交
交![]() 轴于
轴于![]() 点,
点,![]() ,
,![]() 为椭圆
为椭圆![]() 上的动点,
上的动点,![]() 的面积最大值为1.
的面积最大值为1.
(1)求椭圆![]() 的方程;
的方程;
(2)如图,过点![]() 作两条直线与椭圆
作两条直线与椭圆![]() 分别交于
分别交于![]() ,且使
,且使![]() 轴,问四边形
轴,问四边形![]() 的两条对角线的交点是否为定点?若是,求出该定点的坐标;若不是,请说明理由.
的两条对角线的交点是否为定点?若是,求出该定点的坐标;若不是,请说明理由.

【答案】(1)![]() (2)定点坐标为
(2)定点坐标为![]() .
.
【解析】分析:(Ⅰ)![]() 意味着通径的一半
意味着通径的一半![]() ,
,![]() 最大面积为
最大面积为![]() ,所以
,所以![]() ,故椭圆的方程为
,故椭圆的方程为![]() .
.
(Ⅱ)根据对称性,猜测定点必定在![]() 轴上,故可设
轴上,故可设![]() ,
,![]() ,则
,则![]() ,
,![]() ,再设
,再设![]() ,根据
,根据![]() 三点共线可以得到
三点共线可以得到![]() ,联立直线
,联立直线![]() 和椭圆的标准方程后消去
和椭圆的标准方程后消去![]() ,利用韦达定理可以得到
,利用韦达定理可以得到![]() ,从而
,从而![]() 过定点
过定点![]() ,同理直线
,同理直线![]() 也过
也过![]() 即两条直线交于定点
即两条直线交于定点![]() .
.
详解:(Ⅰ)设![]() ,由题意可得
,由题意可得![]() ,即
,即![]() .
.
∵![]() 是
是![]() 的中位线,且
的中位线,且![]() ,
,
∴![]() ,即
,即![]() ,整理得
,整理得![]() .①
.①
又由题知,当![]() 在椭圆
在椭圆![]() 的上顶点时,
的上顶点时,![]() 的面积最大,
的面积最大,
∴![]() ,整理得
,整理得![]() ,即
,即![]() ,②
,②
联立①②可得![]() ,变形得
,变形得![]() ,解得
,解得![]() ,进而
,进而![]() .
.
∴椭圆![]() 的方程式为
的方程式为![]() .
.
(Ⅱ)设![]() ,
,![]() ,则由对称性可知
,则由对称性可知![]() ,
,![]() .
.
设直线![]() 与
与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 的方程为
的方程为![]() ,
,
联立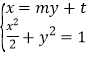 ,消去
,消去![]() ,得
,得![]() ,
,
∴![]() ,
,![]() ,
,
由![]() 三点共线
三点共线![]() ,即
,即![]() ,
,
将![]() ,
,![]() 代入整理得
代入整理得![]() ,
,
即![]() ,从而
,从而![]() ,化简得
,化简得![]() ,解得
,解得![]() ,于是直线
,于是直线![]() 的方程为
的方程为![]() , 故直线
, 故直线![]() 过定点
过定点![]() .同理可得
.同理可得![]() 过定点
过定点![]() ,
,
∴直线![]() 与
与![]() 的交点是定点,定点坐标为
的交点是定点,定点坐标为![]() .
.


 互动英语系列答案
互动英语系列答案科目:高中数学 来源: 题型:
【题目】设函数![]() 是定义在
是定义在![]() 上的偶函数,且
上的偶函数,且![]() 对任意的
对任意的![]() 恒成立,且当
恒成立,且当![]() 时,
时,![]() .
.
(1)求证:![]() 是以2为周期的函数(不需要证明2是
是以2为周期的函数(不需要证明2是![]() 的最小正周期);
的最小正周期);
(2)对于整数![]() ,当
,当![]() 时,求函数
时,求函数![]() 的解析式;
的解析式;
(3)对于整数![]() ,记
,记![]() 在
在![]() 有两个不等的实数根},求集合
有两个不等的实数根},求集合![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某小区抽取50户居民进行月用电量调查,发现其用电量都在50到350度之间,将用电量的数据绘制成频率分布直方图如下.
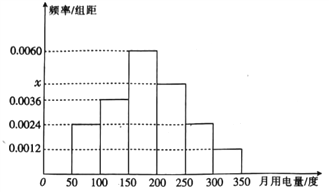
(1)求频率分布直方图中![]() 的值并估计这50户用户的平均用电量;
的值并估计这50户用户的平均用电量;
(2)若将用电量在区间![]() 内的用户记为
内的用户记为![]() 类用户,标记为低用电家庭,用电量在区间
类用户,标记为低用电家庭,用电量在区间![]() 内的用户记为
内的用户记为![]() 类用户,标记为高用电家庭,现对这两类用户进行问卷调查,让其对供电服务进行打分,打分情况见茎叶图:
类用户,标记为高用电家庭,现对这两类用户进行问卷调查,让其对供电服务进行打分,打分情况见茎叶图:
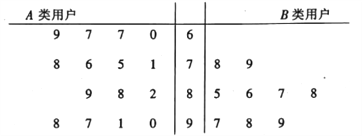
①从![]() 类用户中任意抽取3户,求恰好有2户打分超过85分的概率;
类用户中任意抽取3户,求恰好有2户打分超过85分的概率;
②若打分超过85分视为满意,没超过85分视为不满意,请填写下面列联表,并根据列联表判断是否有![]() 的把握认为“满意度与用电量高低有关”?
的把握认为“满意度与用电量高低有关”?
满意 | 不满意 | 合计 | |
| |||
| |||
合计 |
附表及公式:
| <>0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
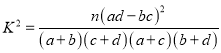 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四名同学各掷骰子5次,分别记录每次骰子出现的点数,根据四名同学的统计结果,可以判断出一定没有出现点数6的是( )
A.平均数为3.中位数为2B.中位数为3.众数为2
C.平均数为2.方差为2.4D.中位数为3.方差为2.8
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知极坐标系的极点与直角坐标系的原点重合,极轴与![]() 轴的非负半轴重合.若曲线
轴的非负半轴重合.若曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为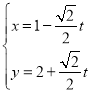 (
(![]() 为参数).
为参数).
(Ⅰ)求曲线![]() 的直角坐标方程与直线
的直角坐标方程与直线![]() 的普通方程;
的普通方程;
(Ⅱ)设点![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一名学生通过计步仪器,记录了自己100天每天走的步数,数据如下:
5678 13039 8666 9521 8722 10575 2107 4165
17073 11205 5467 11736 9986 8592 6542 12386
13115 5705 8358 13234 20142 9769 10426 12802
16722 8587 9266 8635 2455 4524 8260 13165
9812 9533 2377 5132 8212 7968 9859 3961
5484 11344 8722 12944 8597 12594 15101 4751
11130 11286 8897 7192 7313 8790 7699 10892
9583 9207 16358 10182 3607 1789 9417 4566
12347 3228 7606 8689 8755 15609 8767 9226
5622 11094 8865 11246 17417 7995 7317 6878
4270 11051 5705 5442 10078 9107 8354 6483
16808 1509 1301 10843 13864 12691 8419 14267
9809 9858 8922 12682
(1)画出这组数据的频率分布直方图,并分析数据的分布特点;
(2)计算这组数据的平均数、中位数和标准差,并根据这些数值描述这名学生的运动情况.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)判断函数![]() 在区间
在区间![]() 上的单调性,并用定义证明;
上的单调性,并用定义证明;
(2)函数![]() 在区间
在区间![]() 内是否有零点?若有零点,用“二分法”求零点的近似值(精确度0.3);若没有零点,说明理由.
内是否有零点?若有零点,用“二分法”求零点的近似值(精确度0.3);若没有零点,说明理由.
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为棱
为棱![]() 的中点,点
的中点,点![]() 为线段
为线段![]() 上一动点.
上一动点.

(Ⅰ)求证:当点![]() 为线段
为线段![]() 的中点时,
的中点时,![]() 平面
平面![]() ;
;
(Ⅱ)设![]() ,试问:是否存在实数
,试问:是否存在实数![]() ,使得平面
,使得平面![]() 与平面
与平面![]() 所成锐二面角的余弦值为
所成锐二面角的余弦值为![]() ?若存在,求出这个实数
?若存在,求出这个实数![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com