
分析 求解一元二次不等式a2-$\frac{17}{4}$a+1<0得到a的范围,由不等式x2+ax+1>2x+a求出x的范围,结合a的范围得答案.
解答 解:由a2-$\frac{17}{4}$a+1<0,得$\frac{1}{4}<a<4$,即a∈($\frac{1}{4},4$),
∵关于x的不等式x2+ax+1>2x+a对a2-$\frac{17}{4}$a+1<0的一切a恒成立,
∴不等式x2+ax+1>2x+a对a∈($\frac{1}{4},4$)都成立,
由x2+ax+1>2x+a,得x2+(a-2)x+1-a>0,
解得x<1-a或x>1,
∴x≤-3或x>1.
点评 本题考查恒成立问题,考查了不等式的解法,体现了数学转化思想方法,关键是对题意的理解,是中档题.


科目:高中数学 来源: 题型:解答题
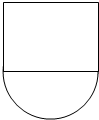 以长为2的铁丝围成上部为矩形,下部为半圆形的框架,如果半圆的直径为2x,求此框架围成图形(如图所示)的面积为y与x的函数关系式y=f(x),并写出它的定义域.
以长为2的铁丝围成上部为矩形,下部为半圆形的框架,如果半圆的直径为2x,求此框架围成图形(如图所示)的面积为y与x的函数关系式y=f(x),并写出它的定义域.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5,10,15,20,25,30 | B. | 2,4,8,16,32,48 | ||
| C. | 1,2,3,4,5,6 | D. | 3,13,23,33,43,53 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 运动员编号 | A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 | A9 | A10 | A11 | A12 |
| 得分 | 5 | 10 | 12 | 16 | 8 | 21 | 27 | 15 | 6 | 22 | 18 |
| 得分区间 | 频数 | 频率 |
| [0,10) | 3 | $\frac{1}{4}$ |
| [10,20) | ||
| [20,30) | ||
| 合计 | 12 | 1.00 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com