
【题目】
直线![]() 的参数方程为
的参数方程为![]() (其中
(其中![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() (其中
(其中![]() ).
).
(1)点![]() 的直角坐标为(2,2),且点
的直角坐标为(2,2),且点![]() 在曲线
在曲线![]() 内,求实数m的取值范围;
内,求实数m的取值范围;
(2)若![]() ,当
,当![]() 变化时,求直线被曲线
变化时,求直线被曲线![]() 截得的弦长的取值范围.
截得的弦长的取值范围.
 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中数学 来源: 题型:
【题目】甲、乙两人2013-2017这五年的年度体检的血压值的折线图如图所示.
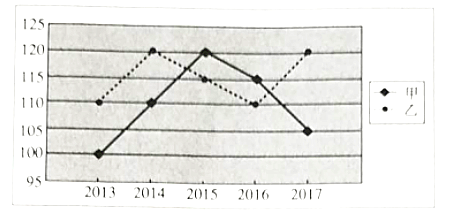
(1)根据散点图,直接判断甲、乙这五年年度体检的血压值谁的波动更大,并求波动更大者的方差;
(2)根据乙这五年年度体检血压值的数据,求年度体检血压值![]() 关于年份
关于年份![]() 的线性回归方程,并据此估计乙在2018年年度体检的血压值.
的线性回归方程,并据此估计乙在2018年年度体检的血压值.
(附: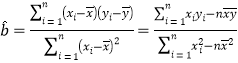 ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年5月20日以来,广东自西北到东南出现了一次明显降雨.为了对某地的降雨情况进行统计,气象部门对当地20日~28日9天内记录了其中100小时的降雨情况,得到每小时降雨情况的频率分布直方图如下:
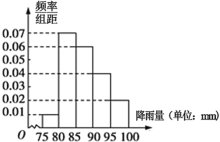
若根据往年防汛经验,每小时降雨量在![]() 时,要保持二级警戒,每小时降雨量在
时,要保持二级警戒,每小时降雨量在![]() 时,要保持一级警戒.
时,要保持一级警戒.
(1)若以每组的中点代表该组数据值,求这100小时内每小时的平均降雨量;
(2)若从记录的这100小时中按照警戒级别采用分层抽样的方法抽取10小时进行深度分析.再从这10小时中随机抽取3小时,求抽取的这3小时中属于一级警戒时间的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年9月24日国家统计局在庆祝中华人民共和国成立70周年活动新闻中心举办新闻发布会指出,1952年~2018年,我国GDP查679.1亿元跃升至90.03万亿元,实际增长174倍;人均GDP从119元提高到6.46万元,实际增长70倍.全国各族人民,砥砺奋进,顽强拼搏,实现了经济社会的跨越式发展.如图是全国2010年至2018年GDP总量![]() (万亿元)的折线图.注:年份代码1~9分别对应年份2010~2018.
(万亿元)的折线图.注:年份代码1~9分别对应年份2010~2018.
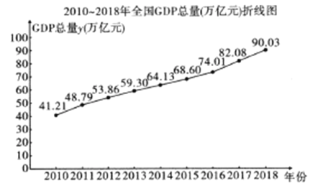
(1)由折线图看出,可用线性回归模型拟合![]() 与年份代码
与年份代码![]() 的关系,请用相关系数加以说明;
的关系,请用相关系数加以说明;
(2)建立![]() 关于
关于![]() 的回归方程(系数精确到0.01),并预测2021年全国GDP的总量.
的回归方程(系数精确到0.01),并预测2021年全国GDP的总量.
附注:参考数据:![]() .
.
参考公式:相关系数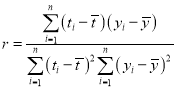 ;
;
回归方程![]() 中斜率和截距的最小二乘法估计公式分别为
中斜率和截距的最小二乘法估计公式分别为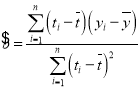 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为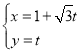 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,圆
轴的非负半轴为极轴建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]()
(1)求圆![]() 的圆心到直线
的圆心到直线![]() 的距离;
的距离;
(2)己知![]() ,若直线
,若直线![]() 与圆
与圆![]() 交于
交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市场研究人员为了了解产业园引进的甲公司前期的经营状况,对该公司2018年连续六个月的利润进行了统计,并根据得到的数据绘制了相应的折线图,如图所示
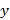
(1)由折线图可以看出,可用线性回归模型拟合月利润![]() (单位:百万元)与月份代码
(单位:百万元)与月份代码![]() 之间的关系,求
之间的关系,求![]() 关于
关于![]() 的线性回归方程,并预测该公司2019年3月份的利润;
的线性回归方程,并预测该公司2019年3月份的利润;
(2)甲公司新研制了一款产品,需要采购一批新型材料,现有![]() ,
,![]() 两种型号的新型材料可供选择,按规定每种新型材料最多可使用
两种型号的新型材料可供选择,按规定每种新型材料最多可使用![]() 个月,但新材料的不稳定性会导致材料损坏的年限不相同,现对
个月,但新材料的不稳定性会导致材料损坏的年限不相同,现对![]() ,
,![]() 两种型号的新型材料对应的产品各
两种型号的新型材料对应的产品各![]() 件进行科学模拟测试,得到两种新型材料使用寿命的频数统计如下表:
件进行科学模拟测试,得到两种新型材料使用寿命的频数统计如下表:
使用寿命 材料类型 |
|
|
|
| 总计 |
|
|
|
|
|
|
|
|
|
|
|
|
如果你是甲公司的负责人,你会选择采购哪款新型材料?
参考数据:![]() ,
,![]() .参考公式:回归直线方程为
.参考公式:回归直线方程为![]() ,其中
,其中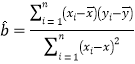
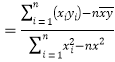 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com