练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    16．某程序框图如图所示，该程序运行后输出S的值是（　　）
    A．22B．25C．28D．31

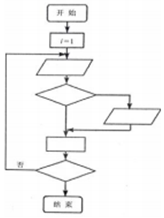
    分析 阅读程序框图知道框图的功能知，每次进入循环体后，S的值被施加的运算是S=S+3，故由此运算规律进行计算，经过8次运算后输出的结果即可．

    解答 解：阅读算法中流程图知：
    运算规则是对S=S+3，故
    第一次进入循环体后S=1+3=4，i=1
    第二次进入循环体后S=3+3=7，i=3
    第三次进入循环体后S=7+3=10，i=7
    第四次进入循环体后S=10+3=13，i=15
    第五次进入循环体后S=13+3=16，i=31
    第六次进入循环体后S=16+3=19，i=63
    第七次进入循环体后S=19+3=22，i=127
    第八次进入循环体后S=22+3=25，i=255
    由i=127＞100，退出循环，输出S=25．
    故选：B．

    点评 本题考查了循环结构的应用问题，解题的关键是读懂框图，能够利用数字进行检验，是基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    6．${（1+x）^5}{（1+\frac{1}{x}）^5}$的展开式中的常数项为252．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．某同学收集了班里9名男生50m跑的测试成绩（单位：s）：
    6，4、7.5、8.0、6.8、9.1、8.3、6.9、8.4、9.5，并设计了一个算法可以从这些数据中搜索出小于8，0的数据，算法步骤如下：
    第一步：i=1
    第二步：输入一个数据a
    第三步：如果a＜8.0，则输出a，否则执行第四步
    第四步：i=i+1
    第五步：如果i＞9，则结束算法，否则执行第二步
    请你根据上述算法将下列程序框图补充完整．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．（Ⅰ）计算：（log29）•（log34）-（2$\sqrt{2}$）${\;}^{\frac{2}{3}}$-eln2；
    （Ⅱ）化简：$\frac{\sqrt{1-sin20°}}{cos10°-sin170°}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．已知平面向量$\overrightarrow{AB}$=（1，y），$\overrightarrow{AC}$=（2，-1），且$\overrightarrow{AB}$$•\overrightarrow{AC}$=0，则3$\overrightarrow{AB}$-2$\overrightarrow{AC}$=（　　）
    A．（8，1）B．（8，3）C．（-1，8）D．（7，8）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    1．如图所示，某几何体的正视图（主视图），侧视图（左视图）和俯视图分别是等腰梯形，等腰直角三角形和长方形，则该几何体表面积为$4\sqrt{2}$+6+$\sqrt{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．设函数f（x）=|x-a|+|x-5|，x∈R．
    （1）当a=2时，求不等式f（x）≥5的解集；
    （2）已知a＜5，若关于x的方程f（x）=ax有且只有两个实数解，求正实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．函数f（x）=3x-$\frac{4}{x}$-a的一个零点在区间（1，2）内，则实数a的取值范围（　　）
    A．（-2，7）B．（-1，6）C．（-1，7）D．（-2，6）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    6．已知双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的右焦点为F（c，0），圆F：（x-c）2+y2=c2，直线l与双曲线C的一条渐近线垂直且在x轴上的截距为$\frac{2}{3}$a，若圆F被直线l所截得的弦长为$\frac{4\sqrt{2}}{3}$c，则双曲线的离心率为2．

    查看答案和解析>>

    同步练习册答案