
分析 判断点A在圆上,用点斜式写出切线方程,求出切线在坐标轴上的截距,从而求出直线与两坐标轴围成的三角形的面积.
解答 解:由题意知,点A在圆上,则A为切点,
∴OA的斜率k=$\frac{1}{2}$,
∴切线斜率为-2,
则切线方程为:y-1=-2(x-2),
即2x+y-5=0,从而求出在两坐标轴上的截距分别是5和$\frac{5}{2}$,
∴所求面积S=$\frac{1}{2}×5×\frac{5}{2}$=$\frac{25}{4}$.
故答案为:$\frac{25}{4}$.
点评 本题考查求圆的切线方程的方法,以及求直线与坐标轴围成的三角形的面积.判断A是切点是解决本题的关键.


科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1.5 | C. | 4 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
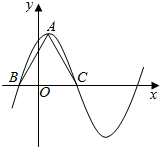 函数f(x)=3cos2$\frac{ωx}{2}$+$\frac{\sqrt{3}}{2}$sinωx-$\frac{3}{2}$(ω>0)在一个周期内的图象如图所示,A为图象的最高点,B、C为图象与x轴的交点,且△ABC为等边三角形.将函数f(x)的图象上各点的横坐标变为原来的π倍,将所得图象向右平移$\frac{2π}{3}$个单位,再向上平移1个单位,得到函数y=g(x)的图象
函数f(x)=3cos2$\frac{ωx}{2}$+$\frac{\sqrt{3}}{2}$sinωx-$\frac{3}{2}$(ω>0)在一个周期内的图象如图所示,A为图象的最高点,B、C为图象与x轴的交点,且△ABC为等边三角形.将函数f(x)的图象上各点的横坐标变为原来的π倍,将所得图象向右平移$\frac{2π}{3}$个单位,再向上平移1个单位,得到函数y=g(x)的图象查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{2}{3}$,1) | B. | (0,$\frac{2}{3}$)∪(1,+∞) | C. | (1,+∞) | D. | (0,$\frac{2}{3}$)∪($\frac{2}{3}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 8 | C. | 14 | D. | 38 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 商品零售额 | 9.5 | 11.5 | 13.5 | 15.5 | 17.5 | 19.5 | 21.5 | 23.5 | 25.5 | 27.5 |
| 商品流通费率 | 6.0 | 4.6 | 4.0 | 3.2 | 2.8 | 2.5 | 2.4 | 2.3 | 2.2 | 2.1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com