
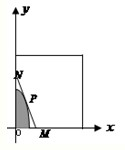
 某建筑公司要在一块宽大的矩形地面(如图所示)上进行开发建设,阴影部分为一公共设施建设不能开发,且要求用栏栅隔开(栏栅要求在一直线上),公共设施边界为曲线f(x)=1-
某建筑公司要在一块宽大的矩形地面(如图所示)上进行开发建设,阴影部分为一公共设施建设不能开发,且要求用栏栅隔开(栏栅要求在一直线上),公共设施边界为曲线f(x)=1-| 4 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 8 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 8 |
| 3 |
| m |
| 2 |
| 3 |
| 8m |
| 4 |
| 3 |
3(1+
| ||
| 16m |
| 3 |
| 16 |
| 1 |
| m |
| 8 |
| 3 |
| 16 |
| 9 |
| 3 |
| 16 |
| 1 |
| m2 |
| 8 |
| 3 |
| 16 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
| 2 |
| 3 |


科目:高中数学 来源: 题型:
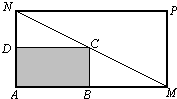 (2008•佛山二模)某物流公司购买了一块长AM=30米、宽AN=20米的矩形地块,规划建设占地如图中矩形ABCD的仓库,其余地方为道路或停车场,要求顶点C在地块对角线MN上,顶点B,D分别在边AM,AN上,设AB长度为x米.
(2008•佛山二模)某物流公司购买了一块长AM=30米、宽AN=20米的矩形地块,规划建设占地如图中矩形ABCD的仓库,其余地方为道路或停车场,要求顶点C在地块对角线MN上,顶点B,D分别在边AM,AN上,设AB长度为x米.查看答案和解析>>
科目:高中数学 来源: 题型:
(08年广东佛山质检文)某物流公司购买了一块长![]() 米,宽
米,宽![]() 米的矩形地块
米的矩形地块![]() ,规划建设占地如图中矩形
,规划建设占地如图中矩形![]() 的仓库,其余地方为道路和停车场,要求顶点
的仓库,其余地方为道路和停车场,要求顶点![]() 在地块对角线
在地块对角线![]() 上,
上,![]() 、
、![]() 分别在边
分别在边![]() 、
、![]() 上,假设
上,假设![]() 长度为
长度为![]() 米.
米.
(1)要使仓库占地![]() 的面积不少于144平方米,
的面积不少于144平方米,![]() 长度应在什么范围内?
长度应在什么范围内?
(2)若规划建设的仓库是高度与![]() 长度相同的长方体形建筑,问
长度相同的长方体形建筑,问![]() 长度为多少时仓库的库容最大?(墙体及楼板所占空间忽略不计)
长度为多少时仓库的库容最大?(墙体及楼板所占空间忽略不计)

查看答案和解析>>
科目:高中数学 来源:2012-2013学年江西省宜春市五校高三(上)12月月考数学试卷(文科)(解析版) 题型:解答题
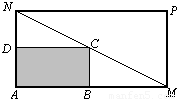 某物流公司购买了一块长AM=30米、宽AN=20米的矩形地块,规划建设占地如图中矩形ABCD的仓库,其余地方为道路或停车场,要求顶点C在地块对角线MN上,顶点B,D分别在边AM,AN上,设AB长度为x米.
某物流公司购买了一块长AM=30米、宽AN=20米的矩形地块,规划建设占地如图中矩形ABCD的仓库,其余地方为道路或停车场,要求顶点C在地块对角线MN上,顶点B,D分别在边AM,AN上,设AB长度为x米.查看答案和解析>>
科目:高中数学 来源:2012-2013学年江西省宜春市五校高三(上)联考数学试卷(文科)(解析版) 题型:解答题
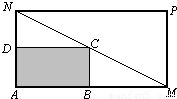 某物流公司购买了一块长AM=30米、宽AN=20米的矩形地块,规划建设占地如图中矩形ABCD的仓库,其余地方为道路或停车场,要求顶点C在地块对角线MN上,顶点B,D分别在边AM,AN上,设AB长度为x米.
某物流公司购买了一块长AM=30米、宽AN=20米的矩形地块,规划建设占地如图中矩形ABCD的仓库,其余地方为道路或停车场,要求顶点C在地块对角线MN上,顶点B,D分别在边AM,AN上,设AB长度为x米.查看答案和解析>>
科目:高中数学 来源:2008年广东省佛山市高考数学二模试卷(文科)(解析版) 题型:解答题
 某物流公司购买了一块长AM=30米、宽AN=20米的矩形地块,规划建设占地如图中矩形ABCD的仓库,其余地方为道路或停车场,要求顶点C在地块对角线MN上,顶点B,D分别在边AM,AN上,设AB长度为x米.
某物流公司购买了一块长AM=30米、宽AN=20米的矩形地块,规划建设占地如图中矩形ABCD的仓库,其余地方为道路或停车场,要求顶点C在地块对角线MN上,顶点B,D分别在边AM,AN上,设AB长度为x米.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com