
| A�� | ��f��3����9���������������k��N*������f��k����k2���� | |
| B�� | ��f��3����9���������������k��3��k��N*������f��k����k2���� | |
| C�� | ��f��3����9���������������k��3��k��N*������f��k����k2���� | |
| D�� | ��f��3��=9���������������k��3��k��N*������f��k����k2���� |
���� ����������Ϻ������������жϼ��ɣ�
��� �⣺A����f��3����9��������f��4����16��������f��k����k2��������k��3�������������жϵ�k=1��2ʱ�Ƿ��������A����
B����f��3����9��������f��4����16��������f��k����k2��������k��3����������B����
C����f��3����9��������f��4����16��������f��k����k2��������k��3����������C����
D����f��3��=9������f��3����9��������f��4����16��������f��k����k2��������k��3����������D��ȷ��
��ѡ��D
���� ������Ҫ�������������Ӧ�ã������������е����ǽ������Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | [$\frac{65}{9}$��25] | B�� | [$\frac{36}{5}$��25] | C�� | [16��25] | D�� | [9��25] |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{��}{3}$ | B�� | $\frac{��}{2}$ | C�� | $\frac{2��}{3}$ | D�� | �� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
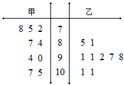 ij���˶���ס�����������˶�Ա�ɼ���ͼ��ʾ���ס��ҵ�ƽ�����ֱ�ΪΪ $\overline{{x}_{��}}$��$\overline{{x}_{��}}$������ֱ�Ϊs��2��s��2��������
ij���˶���ס�����������˶�Ա�ɼ���ͼ��ʾ���ס��ҵ�ƽ�����ֱ�ΪΪ $\overline{{x}_{��}}$��$\overline{{x}_{��}}$������ֱ�Ϊs��2��s��2��������| A�� | $\overline{{x}_{��}}$��$\overline{{x}_{��}}$��s��2��s��2 | B�� | $\overline{{x}_{��}}$��$\overline{{x}_{��}}$��s��2��s��2 | ||
| C�� | $\overline{{x}_{��}}$��$\overline{{x}_{��}}$��s��2��s��2 | D�� | $\overline{{x}_{��}}$��$\overline{{x}_{��}}$��s��2��s��2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
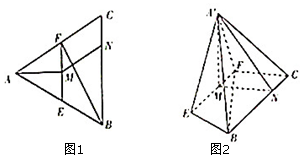 ��ͼ����֪�ȱߡ�ABC�У�E��F�ֱ�ΪAB��AC�ߵ��е㣬MΪEF���е㣬NΪBC����һ�㣬��CN=$\frac{1}{4}$BC������AEF��EF�۵���A'EF��λ�ã�ʹƽ��A'EF��ƽ��EFCB��
��ͼ����֪�ȱߡ�ABC�У�E��F�ֱ�ΪAB��AC�ߵ��е㣬MΪEF���е㣬NΪBC����һ�㣬��CN=$\frac{1}{4}$BC������AEF��EF�۵���A'EF��λ�ã�ʹƽ��A'EF��ƽ��EFCB���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{2}��{R^2}$ | B�� | $\frac{{\sqrt{3}}}{2}��{R^2}$ | C�� | ��R2 | D�� | $\frac{3}{4}��{R^2}$ |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com