
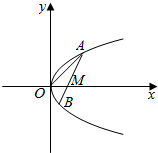
 如图,线段AB过x轴正半轴上一定点M(m,0),端点A、B到x轴距离之积为2m,以x轴为对称轴,过A,O,B三点作抛物线C.
如图,线段AB过x轴正半轴上一定点M(m,0),端点A、B到x轴距离之积为2m,以x轴为对称轴,过A,O,B三点作抛物线C.分析 (1)设抛物线方程、直线AB的方程,联立这两个方程组消去x,利用两端点A、B到x轴的距离之积为2m,可求m的值,从而可得抛物线方程;
(2)由S(x1,y1),T(x2,y2)在抛物线y2=2x上,得到两方程,作差,结合斜率公式,可得ST的斜率,同理可得PS,PT的斜率,由kSP=-kPT,可得y1+y2=-4,由此能够证明直线ST的斜率为定值.
解答 (1)解:可设抛物线方程为y2=2px(p>0),
设直线AB的方程为y=k(x-m)(k≠0)…(2分)
联立这两个方程组消去x得,ky2-2py-2pkm=0,…(4分)
设A(x1,y1),B(x2,y2),由已知得|y1|•|y2|=2m,注意到y1•y2<0,所以y1•y2=-2m,
又y1•y2=-2pm,所以-2m=-2pm,因为m>0,所以p=1.
所以抛物线方程为y2=2x;…(6分)
(2)证明:∵点P(n,2)为抛物线C上的点,∴n=2,∴P(2,2).
∵S(x1,y1),T(x2,y2)在抛物线y2=2x上,
∴y12=2x1,y22=2x2,
∴y12-y22=2(x1-x2),
∵x1≠x2,
∴kST=$\frac{2}{{y}_{1}+{y}_{2}}$,
同理,kSP=$\frac{2}{{y}_{1}+2}$,kPT=$\frac{2}{{y}_{2}+2}$,
∵kSP=-kPT,
∴$\frac{2}{{y}_{1}+2}$=-$\frac{2}{{y}_{2}+2}$,
∴y1+y2=-4,
故直线ST的斜率kST=-$\frac{1}{2}$(定值).
点评 本题考查抛物线的标准方程,考查直线与抛物线的位置关系,考查韦达定理的运用,考查运算求解能力,推理论证能力;考查化归与转化思想.对数学思维的要求比较高,有一定的探索性.综合性强,是高考的重点.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 72 | B. | 71 | C. | 73 | D. | 74 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{5}$-1 | B. | 2$+\sqrt{5}$ | C. | 3$+\sqrt{5}$ | D. | 5$+\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 关于点($\frac{π}{4}$,0)中心对称 | B. | 关于点($\frac{π}{2}$,0)中心对称 | ||
| C. | 关于点($\frac{3π}{4}$,0)中心对称 | D. | 关于点(π,0)中心对称 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知函数f(x)是定义在R上的奇函数,已知x≥0时,f(x)=x(2-x).
已知函数f(x)是定义在R上的奇函数,已知x≥0时,f(x)=x(2-x).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com