
【题目】已知函数![]() .
.
(1)证明函数![]() 在
在![]() 上为减函数;
上为减函数;
(2)求函数![]() 的定义域,并求其奇偶性;
的定义域,并求其奇偶性;
(3)若存在![]() ,使得不等式
,使得不等式![]() 能成立,试求实数a的取值范围.
能成立,试求实数a的取值范围.
【答案】(1)证明见解析;(2)![]() ,奇函数;(3)
,奇函数;(3)![]() .
.
【解析】
(1)利用单调性定义证明即可.
(2)根据条件可得![]() ,其解集即为函数的定义域,可判断定义域关于原点对称,再根据奇偶性定义可判断函数的奇偶性.
,其解集即为函数的定义域,可判断定义域关于原点对称,再根据奇偶性定义可判断函数的奇偶性.
(3)令![]() ,考虑
,考虑![]() 在
在![]() 上有解即可,参变分离后利用基本不等式可求实数
上有解即可,参变分离后利用基本不等式可求实数![]() 的取值范围.
的取值范围.
(1)![]() ,
,![]() ,
,![]() ,
,
又 ,
,
因为![]() ,
,![]() ,
,![]() ,故
,故![]() ,
,![]() ,
,![]() ,
,
故![]() 即
即![]() ,所以函数
,所以函数![]() 在
在![]() 上为减函数.
上为减函数.
(2)![]() 的
的![]() 满足的不等关系有:
满足的不等关系有:![]() 即
即![]() ,
,
故![]() ,解得
,解得![]() ,
,
故函数的定义域为![]() ,
,![]() ,该定义域关于原点对称.
,该定义域关于原点对称.
令![]()
又![]()
![]() ,
,
故![]() 为奇函数.
为奇函数.
(3)令![]() ,因为
,因为![]() ,故
,故![]() .
.
故在![]() 上不等式
上不等式![]() 能成立即为
能成立即为
存在![]() ,使得
,使得![]() ,所以
,所以![]() 在
在![]() 上能成立,
上能成立,
令![]() ,则
,则![]() 且
且 ,
,
由基本不等式有![]() ,当且仅当
,当且仅当![]() 时等号成立,
时等号成立,
所以![]() ,当且仅当
,当且仅当![]() 时等号成立,
时等号成立,
故![]() 的最大值为
的最大值为![]() ,所以a的取值范围为
,所以a的取值范围为![]() .
.


 阶梯计算系列答案
阶梯计算系列答案科目:高中数学 来源: 题型:
【题目】国家质量监督检验检疫局于2004年5月31日发布了新的《车辆驾驶人员血液、呼吸酒精含量阀值与检验》国家标准,新标准规定,车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升,小于80毫克/百毫克升为饮酒驾车,血液中的酒精含量大于或等于80毫克/百毫升为醉酒驾车,经过反复试验,喝1瓶啤酒后酒精在人体血液中的变化规律的“散点图”如下:
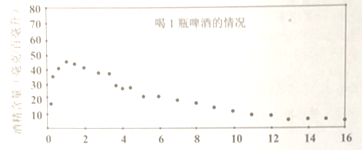
该函数模型如下:
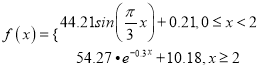
根据上述条件,回答以下问题:
(1)试计算喝1瓶啤酒后多少小时血液中的酒精含量达到最大值?最大值是多少?
(2)试计算喝1瓶啤酒后多少小时后才可以驾车?(时间以整小时计算)
(参数数据: ![]() ,
, ![]() ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(江苏省南京师大附中2018届高三高考考前模拟考试数学试题)已知函数f(x)=lnx-ax+a,a∈R.
(1)若a=1,求函数f(x)的极值;
(2)若函数f(x)有两个零点,求a的范围;
(3)对于曲线y=f(x)上的两个不同的点P(x1,f(x1)),Q(x2,f(x2)),记直线PQ的斜率为k,若y=f(x)的导函数为f ′(x),证明:f ′(![]() )<k.
)<k.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】空气质量指数AQI是反映空气质量状况的指数,AQI指数值越小,表明空气质量越好,其对应关系如下表:
AQI指数值 | 0~50 | 51~100 | 101~150 | 151~200 | 201~300 | >300 |
空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
下图是某市10月1日—20日AQI指数变化趋势:

下列叙述错误的是
A. 这20天中AQI指数值的中位数略高于100
B. 这20天中的中度污染及以上的天数占![]()
C. 该市10月的前半个月的空气质量越来越好
D. 总体来说,该市10月上旬的空气质量比中旬的空气质量好
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,当
,当![]() 时,
时,![]() .
.
(Ⅰ)若函数![]() 过点
过点![]() ,求此时函数
,求此时函数![]() 的解析式;
的解析式;
(Ⅱ)若函数![]() 只有一个零点,求实数
只有一个零点,求实数![]() 的值;
的值;
(Ⅲ)设![]() ,若对任意实数
,若对任意实数![]() ,函数
,函数![]() 在
在![]() 上的最大值与最小值的差不大于1,求实数
上的最大值与最小值的差不大于1,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】受日月引力影响,海水会发生涨退潮现象.通常情况下,船在涨潮时驶进港口,退潮时离开港口.某港口在某季节每天港口水位的深度![]() (米)是时间
(米)是时间![]() (
(![]() ,单位:小时,
,单位:小时,![]() 表示0:00—零时)的函数,其函数关系式为
表示0:00—零时)的函数,其函数关系式为![]()
![]()
![]() .已知一天中该港口水位的深度变化有如下规律:出现相邻两次最高水位的深度的时间差为12小时,最高水位的深度为12米,最低水位的深度为6米,每天13:00时港口水位的深度恰为10.5米.
.已知一天中该港口水位的深度变化有如下规律:出现相邻两次最高水位的深度的时间差为12小时,最高水位的深度为12米,最低水位的深度为6米,每天13:00时港口水位的深度恰为10.5米.
(1)试求函数![]() 的表达式;
的表达式;
(2)某货船的吃水深度(船底与水面的距离)为7米,安全条例规定船舶航行时船底与海底的距离不小于3.5米是安全的,问该船在当天的什么时间段能够安全进港?若该船欲于当天安全离港,则它最迟应在当天几点以前离开港口?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E: ![]() (a﹥b﹥0)的一个焦点与短轴的两个端点是正三角形的三个顶点,点
(a﹥b﹥0)的一个焦点与短轴的两个端点是正三角形的三个顶点,点![]() 在椭圆E上.
在椭圆E上.
(Ⅰ)求椭圆E的方程;
(Ⅱ)设不过原点O且斜率为![]() 的直线l与椭圆E交于不同的两点A,B,线段AB的中点为M,直线OM与椭圆E交于C,D,证明:|MA|·|MB|=|MC|·|MD|.
的直线l与椭圆E交于不同的两点A,B,线段AB的中点为M,直线OM与椭圆E交于C,D,证明:|MA|·|MB|=|MC|·|MD|.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com