
【题目】已知圆![]() 的圆心在
的圆心在![]() 轴上,点
轴上,点![]() 是圆
是圆![]() 的上任一点,且当点
的上任一点,且当点![]() 的坐标为
的坐标为![]() 时,
时,![]() 到直线
到直线![]() 距离最大.
距离最大.
(1)求直线![]() 被圆
被圆![]() 截得的弦长;
截得的弦长;
(2)已知![]() ,经过原点,且斜率为
,经过原点,且斜率为![]() 的直线
的直线![]() 与圆
与圆![]() 交于
交于![]() ,
,![]() 两点.
两点.
(Ⅰ)求证:![]() 为定值;
为定值;
(Ⅱ)若![]() ,求直线
,求直线![]() 的方程.
的方程.
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() . (I)求函数f(x)的单调区间;
. (I)求函数f(x)的单调区间;
(II)若不等式f(x)> ![]() 恒成立,求整数k的最大值;
恒成立,求整数k的最大值;
(III)求证:(1+1×2)(1+2×3)…(1+n(n×1))>e2n﹣3(n∈N*).
查看答案和解析>>
科目:高中数学 来源: 题型:
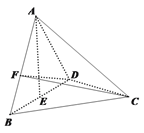
【题目】如图,在三棱锥![]() 中,已知
中,已知![]() 都是边长为
都是边长为![]() 的等边三角形,
的等边三角形,![]() 为
为![]() 中点,且
中点,且![]() 平面
平面![]() ,
,![]() 为线段
为线段![]() 上一动点,记
上一动点,记![]() .
.
(1)当![]() 时,求异面直线
时,求异面直线![]() 与
与![]() 所成角的余弦值;
所成角的余弦值;
(2)当![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知顶点为原点O的抛物线C1的焦点F与椭圆C2: ![]() =1(a>b>0)的右焦点重合,C1与C2在第一和第四象限的交点分别为A、B.
=1(a>b>0)的右焦点重合,C1与C2在第一和第四象限的交点分别为A、B.
(1)若△AOB是边长为2 ![]() 的正三角形,求抛物线C1的方程;
的正三角形,求抛物线C1的方程;
(2)若AF⊥OF,求椭圆C2的离心率e;
(3)点P为椭圆C2上的任一点,若直线AP、BP分别与x轴交于点M(m,0)和N(n,0),证明:mn=a2 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为Aa,b,c,且满足 ![]() =
= ![]()
(1)若4sinC=c2sinB,求△ABC的面积;
(2)若 ![]()
![]() +
+ ![]() =4,求a的最小值.
=4,求a的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“傻子瓜子”是著名瓜子品牌,芜湖特产之一.屯溪一中组织高二年级赴芜湖方特进 行研学活动,开拓视野,甲、乙两名同学在活动结束之余准备赴商场购买一定量的傻子瓜子.为了让本次研学活动具有实际意义,两名同学经过了解得知![]() 系列的瓜子不仅便宜而且口味还不错,并且每日的销售量
系列的瓜子不仅便宜而且口味还不错,并且每日的销售量![]() (单位:千克)与销售价格
(单位:千克)与销售价格![]() (元/千克)满足关系式:
(元/千克)满足关系式:![]() ,其中
,其中![]() ,
,![]() 为常数.已知销售价格为5元/千克时,每日可售出
为常数.已知销售价格为5元/千克时,每日可售出![]() 系列瓜子11千克.若
系列瓜子11千克.若![]() 系列瓜子的成本为3元/千克,试确定销售价格
系列瓜子的成本为3元/千克,试确定销售价格![]() 的值,使该商场每日销售
的值,使该商场每日销售![]() 系列瓜子所获得的利润最大.
系列瓜子所获得的利润最大.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com