
【题目】已知定义在R上的偶函数满足:f(x+4)=f(x)+f(2),且当x∈[0,2]时,y=f(x)单调递减,给出以下四个命题:
①f(2)=0;
②x=﹣4为函数y=f(x)图象的一条对称轴;
③函数y=f(x)在[8,10]单调递增;
④若方程f(x)=m在[﹣6,﹣2]上的两根为x1 , x2 , 则x1+x2=﹣8.
上述命题中所有正确命题的序号为 .
【答案】①②④
【解析】解:∵f(x)是定义在R上的偶函数,
∴f(﹣x)=f(x),
可得f(﹣2)=f(2),
在f(x+4)=f(x)+f(2),中令x=﹣2得
f(2)=f(﹣2)+f(2),
∴f(﹣2)=f(2)=0,
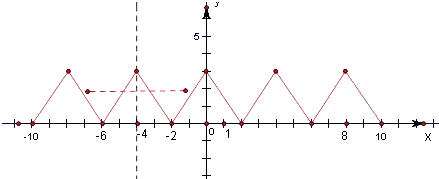
∴f(x+4)=f(x),∴函数f(x)是周期为4的周期函数,又当x∈[0,2]时,y=f(x)单调递减,结合函数的奇偶性画出函数f(x)的简图,如图所示.
从图中可以得出:
②x=﹣4为函数y=f(x)图象的一条对称轴;
③函数y=f(x)在[8,10]单调递减;
④若方程f(x)=m在[﹣6,﹣2]上的两根为x1,x2,则x1+x2=﹣8.
所以答案是:①②④.
【考点精析】解答此题的关键在于理解命题的真假判断与应用的相关知识,掌握两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系,以及对函数单调性的判断方法的理解,了解单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:高中数学 来源: 题型:
【题目】设n≥3,n∈N* , 在集合{1,2,…,n}的所有元素个数为2的子集中,把每个子集的较大元素相加,和记为a,较小元素之和记为b.
(1)当n=3时,求a,b的值;
(2)求证:对任意的n≥3,n∈N* , ![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区拟建立一个艺术搏物馆,采取竞标的方式从多家建筑公司选取一家建筑公司,经过层层筛选,甲、乙两家建筑公司进入最后的招标.现从建筑设计院聘请专家设计了一个招标方案:两家公司从6个招标总是中随机抽取3个总题,已知这6个招标问题中,甲公司可正确回答其中4道题目,而乙公司能正面回答每道题目的概率均为 ![]() ,甲、乙两家公司对每题的回答都是相独立,互不影响的.
,甲、乙两家公司对每题的回答都是相独立,互不影响的.
(1)求甲、乙两家公司共答对2道题目的概率;
(2)请从期望和方差的角度分析,甲、乙两家哪家公司竞标成功的可能性更大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:(x﹣3)2+(y﹣4)2=4,直线l过定点A(1,0).
(1)若l与圆C相切,求l的方程;
(2)若l与圆C相交于P、Q两点,若|PQ|=2 ![]() ,求此时直线l的方程.
,求此时直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的图象与函数h(x)=x+ ![]() +2的图象关于点A(0,1)对称.
+2的图象关于点A(0,1)对称.
(1)求f(x)的解析式;
(2)若g(x)=f(x)x+ax,且g(x)在区间[0,2]上为减函数,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《聊斋志异》中有这样一首诗:“挑水砍柴不堪苦,请归但求穿墙术.得诀自诩无所阻,额上坟起终不悟.”在这里,我们称形如以下形式的等式具有“穿墙术”: 2 ![]() =
= ![]() ,3
,3 ![]() =
= ![]() ,4
,4 ![]() =
= ![]() ,5
,5 ![]() =
= ![]()
则按照以上规律,若8 ![]() =
= ![]() 具有“穿墙术”,则n=( )
具有“穿墙术”,则n=( )
A.7
B.35
C.48
D.63
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com