练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    在△ABC中，已知锐角B所对边b＝7，外接圆半径，三角形面积S＝10，求三角形其他两边的长．

    答案：
    解析：

    a＝5，c＝8或a＝8，c＝5．


    提示：

    　　[提示]利用三角形面积公式和正弦定理，结合已知条件，可求出ac和角B的值，就可以运用余弦定理来解三角形了．

    　　[说明]正弦定理有如下几种变式：

    　　(1)a＝2RsinA，b＝2RsinB，c＝2RsinC；

    　　(2)sinA＝，sinB＝，sinC＝；

    　　(3)sinA∶sinB∶sinC＝a∶b∶c(R为△ABC外接圆半径)．

    　　解题时要注意灵活运用．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

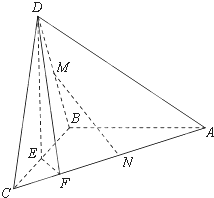    如图，在三棱锥D-ABC中，已知△BCD是正三角形，AB⊥平面BCD，AB=BC，E为BC的中点，F在棱AC上，且AF=3FC．
    （1）求证：AC⊥平面DEF；
    （2）求平面DEF与平面ABD所成的锐二面角的余弦值；
    （3）若M为BD的中点，问AC上是否存在一点N，使MN∥平面DEF？若存在，说明点N的位置；若不存在，试说明理由．

    查看答案和解析>>

    科目：高中数学 来源：2010-2011年浙江省高二下学期期中考试数学2-4 题型：解答题

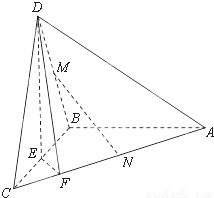
    如图，在三棱锥D－ABC中，已知△BCD是正三角形，AB⊥平面BCD，AB＝BC＝a，E为BC的中点，F在棱AC上，且AF＝3FC．

    （1）求证AC⊥平面DEF；

    （2）若M为BD的中点，问AC上是否存在一点N，使MN∥平面DEF？若存在，说明点N的位置；若不存在，试说明理由．

    （3）求平面ABD与平面DEF所成锐二面角的余弦值。

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

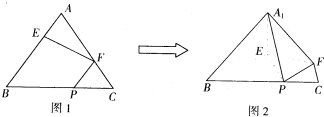    如图1，在正三角形ABC中，已知AB=5，E、F、P分别是AB、AC、BC边上的点，设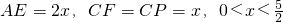数学公式，将△ABC沿EF折起到△A1EF的位置，使二面角A1-EF-B的大小为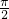数学公式，连接A1B、A1P（如图2）．
    （1）求证：PF∥平面A1EB；
    （2）若EF⊥平面A1EB，求x的值；
    （3）当EF⊥平面A1EB时，求平面A1BP与平面A1EF所成锐二面角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源：0103 期末题 题型：解答题

    如图，在三棱锥D-ABC中，已知△BCD是正三角形，AB⊥平面BCD，AB=BC，E为BC的中点，F在棱AC上，且AF=3FC，
    （1）求证：AC⊥平面DEF；
    （2）求平面DEF与平面ABD所成的锐二面角的余弦值；
    （3）若M为BD的中点，问AC上是否存在一点N，使MN∥平面DEF？若存在，说明点N的位置；若不存在，试说明理由。

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年浙江省衢州市江山实验中学高二（上）12月月考数学试卷（文科）（解析版） 题型：解答题

    如图，在三棱锥D-ABC中，已知△BCD是正三角形，AB⊥平面BCD，AB=BC，E为BC的中点，F在棱AC上，且AF=3FC．
    （1）求证：AC⊥平面DEF；
    （2）求平面DEF与平面ABD所成的锐二面角的余弦值；
    （3）若M为BD的中点，问AC上是否存在一点N，使MN∥平面DEF？若存在，说明点N的位置；若不存在，试说明理由．

    查看答案和解析>>

    同步练习册答案