
【题目】(理科答)已知数列{an}及等差数列{bn},若a1=3,an= ![]() an﹣1+1(n≥2),a1=b2 , 2a3+a2=b4 ,
an﹣1+1(n≥2),a1=b2 , 2a3+a2=b4 ,
(1)证明数列{an﹣2}为等比数列;
(2)求数列{an}及数列{bn}的通项公式;
(3)设数列{anbn}的前n项和为Tn , 求Tn .
【答案】
(1)证明:a1=3,an= ![]() an﹣1+1(n≥2),
an﹣1+1(n≥2),
an﹣2= ![]() (an﹣1﹣2),
(an﹣1﹣2),
则数列{an﹣2}为首项为1,公比为 ![]() 的等比数列
的等比数列
(2)解:(由(1)可得an﹣2=( ![]() )n﹣1,
)n﹣1,
即为an=2+( ![]() )n﹣1,
)n﹣1,
a1=b2=3,
2a3+a2=b4=2(2+ ![]() )+2+
)+2+ ![]() =7,
=7,
可得等差数列{bn}的公差d= ![]() =2,
=2,
则bn=b2+(n﹣2)d=3+2(n﹣2)=2n﹣1
(3)证明:数列{anbn}的前n项和为Tn,
anbn=[2+( ![]() )n﹣1](2n﹣1)=2(2n﹣1)+(2n﹣1)(
)n﹣1](2n﹣1)=2(2n﹣1)+(2n﹣1)( ![]() )n﹣1,
)n﹣1,
设Sn=1( ![]() )0+3(
)0+3( ![]() )+5(
)+5( ![]() )2+…+(2n﹣1)(
)2+…+(2n﹣1)( ![]() )n﹣1,
)n﹣1,
![]() Sn=1(
Sn=1( ![]() )+3(
)+3( ![]() )2+5(
)2+5( ![]() )3+…+(2n﹣1)(
)3+…+(2n﹣1)( ![]() )n,
)n,
相减可得, ![]() Sn=1+2[(
Sn=1+2[( ![]() )+(
)+( ![]() )2+(
)2+( ![]() )3+…+(
)3+…+( ![]() )n﹣1]﹣(2n﹣1)(
)n﹣1]﹣(2n﹣1)( ![]() )n
)n
=1+2[ 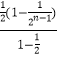 ]﹣(2n﹣1)(
]﹣(2n﹣1)( ![]() )n,
)n,
化简可得Sn=6﹣ ![]() ,
,
则Tn=2 ![]() n(1+2n﹣1)+6﹣
n(1+2n﹣1)+6﹣ ![]() =2n2+6﹣
=2n2+6﹣ ![]()
【解析】(1)an= ![]() an﹣1+1的两边减2,再由等比数列的定义即可得证;(2)运用等比数列和等差数列的通项公式,计算即可得到;(3)求得anbn=[2+(
an﹣1+1的两边减2,再由等比数列的定义即可得证;(2)运用等比数列和等差数列的通项公式,计算即可得到;(3)求得anbn=[2+( ![]() )n﹣1](2n﹣1)=2(2n﹣1)+(2n﹣1)(
)n﹣1](2n﹣1)=2(2n﹣1)+(2n﹣1)( ![]() )n﹣1 , 再由数列的求和方法:分组求和和错位相减法,结合等比数列的求和公式,化简整理即可得到所求和.
)n﹣1 , 再由数列的求和方法:分组求和和错位相减法,结合等比数列的求和公式,化简整理即可得到所求和.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:高中数学 来源: 题型:
【题目】某种新产品投放市场的100天中,前40天价格呈直线上升,而后60天其价格呈直线下降,现统计出其中4天的价格如下表:
时间 | 第4天 | 第32天 | 第60天 | 第90天 |
价格(千元) | 23 | 30 | 22 | 7 |
(Ⅰ)写出价格f(x)关于时间x的函数关系式(x表示投放市场的第x天,x∈N*);
(Ⅱ)销售量g(x)与时间x的函数关系式为 ![]() ,则该产品投放市场第几天的销售额最高?最高为多少千元?
,则该产品投放市场第几天的销售额最高?最高为多少千元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}和{bn}(bn≠0,n∈N*),满足a1=b1=1,anbn+1﹣an+1bn+bn+1bn=0
(1)令cn= ![]() ,证明数列{cn}是等差数列,并求{cn}的通项公式
,证明数列{cn}是等差数列,并求{cn}的通项公式
(2)若bn=2n﹣1 , 求数列{an}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() 的展开式各项系数和为M,
的展开式各项系数和为M, ![]() 的展开式各项系数和为N,(x+1)n的展开式各项的系数和为P,且M+N﹣P=2016,试求
的展开式各项系数和为N,(x+1)n的展开式各项的系数和为P,且M+N﹣P=2016,试求 ![]() 的展开式中:
的展开式中:
(1)二项式系数最大的项;
(2)系数的绝对值最大的项.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种汽车,购车费用是10万元,每年使用的保险费、养路费、汽车费约为0.9万元,年维修费第一年是0.2万元,以后逐年递增0.2万元,问这种汽车使用多少年时,它的平均费用最少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学用“五点法”画函数f(x)=Asin(ωx+φ)(ω>0,|φ|< ![]() )在某一个周期内的图象时,列表并填入了部分数据,如表:
)在某一个周期内的图象时,列表并填入了部分数据,如表:
ωx+φ | 0 |
| π |
| 2π |
x |
|
| |||
Asin(ωx+φ) | 0 | 5 | ﹣5 | 0 |
(1)请将上表数据补充完整,填写在相应位置,并直接写出函数f(x)的解析式;
(2)将y=f(x)图象上所有点向左平行移动θ(θ>0)个单位长度,得到y=g(x)的图象.若y=g(x)图象的一个对称中心为( ![]() ,0),求θ的最小值.
,0),求θ的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>b>0)过点(
=1(a>b>0)过点( ![]() ,﹣
,﹣ ![]() ),且离心率为
),且离心率为 ![]() . (Ⅰ)求椭圆C的标准方程;
. (Ⅰ)求椭圆C的标准方程;
(Ⅱ)若点A(x1 , y1),B(x2 , y2)是椭圆C上的亮点,且x1≠x2 , 点P(1,0),证明:△PAB不可能为等边三角形.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在我国古代著名的数学专著《九章算术》里有﹣段叙述:今有良马与驽马发长安至齐,齐去长安一千一百二十五里,良马初日行一百零三里,日增十三里:驽马初日行九十七里,日减半里,良马先至齐,复还迎驽马,二马相逢,问:需日相逢.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com