
【题目】若对任意的正整数![]() ,总存在正整数
,总存在正整数![]() ,使得数列
,使得数列![]() 的前
的前![]() 项和
项和![]() ,则称数列
,则称数列![]() 是“回归数列”.
是“回归数列”.
(1)前![]() 项和为
项和为![]() 的数列
的数列![]() 是否是“回归数列”?并请说明理由;
是否是“回归数列”?并请说明理由;
(2)设![]() 是等差数列,首项
是等差数列,首项![]() ,公差
,公差![]() ,若
,若![]() 是“回归数列”,求
是“回归数列”,求![]() 的值;
的值;
(3)是否对任意的等差数列![]() ,总存在两个“回归数列”
,总存在两个“回归数列”![]() 和
和![]() ,使得
,使得![]() (
(![]() )成立,请给出你的结论,并说明理由.
)成立,请给出你的结论,并说明理由.
【答案】(1)是;(2)![]() ;(3)存在,理由见解析.
;(3)存在,理由见解析.
【解析】
(1)由题意,根据数列中![]() 与
与![]() ,分别的奥
,分别的奥![]() 和
和![]() 时,对任意的
时,对任意的![]() 存在正整数
存在正整数![]() 使得
使得![]() 成立,解得结论;
成立,解得结论;
(2)因为![]() 是等差数列,首项
是等差数列,首项![]() ,公差
,公差![]() ,则对任意的
,则对任意的![]() 存在正整数
存在正整数![]() 使得
使得![]() 成立,现求得当
成立,现求得当![]() 时,得到
时,得到![]() ,再验证
,再验证![]() 时,对任意的
时,对任意的![]() 存在正整数
存在正整数![]() 使得
使得![]() 成立,即可得到结论。
成立,即可得到结论。
(3)由(2)知,可以构造一个回归的等差数列![]() ,验证
,验证![]() 时,得到
时,得到![]() ,使得
,使得![]() 成立,进而对于对任意等差数列
成立,进而对于对任意等差数列![]() ,得到
,得到![]() ,使得
,使得![]() 成立,即可得到答案。
成立,即可得到答案。
(1)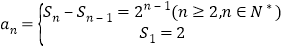
显然
![]() 时,存在正整数
时,存在正整数![]() 使得
使得![]() 成立符合题意
成立符合题意
![]() 时,对任意的
时,对任意的![]() 存在正整数
存在正整数![]() 使得
使得![]() 成立
成立
(2)因为![]() 是等差数列,首项
是等差数列,首项![]() ,公差
,公差![]()
所以对任意的![]() 存在正整数
存在正整数![]() 使得
使得![]() 成立
成立
当![]() 时
时![]() ,公差
,公差![]() ,所以正整数
,所以正整数![]() 只能是1,所以
只能是1,所以![]()
验证:![]() 时,对任意的
时,对任意的![]() 存在正整数
存在正整数![]() 使得
使得![]() 成立
成立
(3)由(2)知,可以构造一个回归的等差数列![]()
验证:
![]() 时,
时,![]() 是奇数,
是奇数,![]() 是偶数,
是偶数,![]() 是偶数,
是偶数,![]() 是奇数,
是奇数,![]()
对任意的![]() 存在正整数
存在正整数![]() ,使得
,使得![]() 成立
成立
对任意的一个等差数列![]() ,
,
一定得到![]()
![]() 是常数,
是常数,![]() 是等差数列,首项为0
是等差数列,首项为0
任意的![]() ,它的前
,它的前![]() 项和
项和![]() ,假设它是回归数列,则存在正整数
,假设它是回归数列,则存在正整数![]() 使2得
使2得![]() 成立,
成立,![]() 成立
成立
解得![]()


科目:高中数学 来源: 题型:
【题目】2018年8月31日,十三届全国人大常委会第五次会议表决通过了关于修改个人所得税法的决定,这是我国个人所得税法自1980年出台以来第七次大修![]() 为了让纳税人尽早享受减税红利,在过渡期对纳税个人按照下表计算个人所得税,值得注意的是起征点变为5000元,即如表中“全月应纳税所得额”是纳税者的月薪金收入减去5000元后的余额.
为了让纳税人尽早享受减税红利,在过渡期对纳税个人按照下表计算个人所得税,值得注意的是起征点变为5000元,即如表中“全月应纳税所得额”是纳税者的月薪金收入减去5000元后的余额.
级数 | 全月应纳税所得额 | 税率 |
1 | 不超过3000元的部分 |
|
2 | 超过3000元至12000元的部分 |
|
3 | 超过12000元至25000元的部分 |
|
|
|
|
某企业员工今年10月份的月工资为15000元,则应缴纳的个人所得税为______元![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2名女生、4名男生排成一排,求:
(1)2名女生不相邻的不同排法共有多少种?
(2)女生甲必须排在女生乙的左边(不一定相邻)的不同排法共有多少种?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】天干地支纪年法,源于中国,中国自古便有十天干与十二地支.十天干:甲、乙、丙、丁、戊、己、庚、辛、壬、癸.十二地支:子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥.天干地支纪年法是按顺序以一个天干和一个地支相配,排列起来,天干在前,地支在后,天干由“甲”起,地支由“子”起,比如第一年为“甲子”,第二年为“乙丑”,第三年为“丙寅”,…,以此类推,排列到“癸酉”后,天干回到“甲”重新开始,即“甲戌”,“乙亥”,之后地支回到“子”重新开始,即“丙子”,…,以此类推,已知2016年为丙申年,那么到改革开放100年时,即2078年为________年
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 上的
上的![]() 、
、![]() 两点满足
两点满足![]() ,点
,点![]() 、
、![]() 在抛物线对称轴的左右两侧,且
在抛物线对称轴的左右两侧,且![]() 的横坐标小于零,抛物线顶点为
的横坐标小于零,抛物线顶点为![]() ,焦点为
,焦点为![]() .
.
(1)当点![]() 的横坐标为2,求点
的横坐标为2,求点![]() 的坐标;
的坐标;
(2)抛物线上是否存在点![]() ,使得
,使得![]() (
(![]() ),若请说明理由;
),若请说明理由;
(3)设焦点![]() 关于直线
关于直线![]() 的对称点是
的对称点是![]() ,求当四边形
,求当四边形![]() 面积最小值时点
面积最小值时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国家质量监督检验检疫局于2004年5月31日发布了新的《车辆驾驶人员血液、呼吸酒精含量阀值与检验》国家标准,新标准规定,车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升,小于80毫克/百毫克升为饮酒驾车,血液中的酒精含量大于或等于80毫克/百毫升为醉酒驾车,经过反复试验,喝1瓶啤酒后酒精在人体血液中的变化规律的“散点图”如下:

该函数模型如下:

根据上述条件,回答以下问题:
(1)试计算喝1瓶啤酒后多少小时血液中的酒精含量达到最大值?最大值是多少?
(2)试计算喝1瓶啤酒后多少小时后才可以驾车?(时间以整小时计算)
(参数数据: ![]() ,
, ![]() ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
在平面直角坐标系xOy中,点B与点A(-1,1)关于原点O对称,P是动点,且直线AP与BP的斜率之积等于![]() .
.
(Ⅰ)求动点P的轨迹方程;
(Ⅱ)设直线AP和BP分别与直线x=3交于点M,N,问:是否存在点P使得△PAB与△PMN的面积相等?若存在,求出点P的坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2017·全国卷Ⅲ文,18)某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间[20,25),需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:
最高气温 | [10,15) | [15,20) | [20,25) | [25,30) | [30,35) | [35,40) |
天数 | 2 | 16 | 36 | 25 | 7 | 4 |
以最高气温位于各区间的频率估计最高气温位于该区间的概率.
(1)估计六月份这种酸奶一天的需求量不超过300瓶的概率;
(2)设六月份一天销售这种酸奶的利润为Y(单位:元).当六月份这种酸奶一天的进货量为450瓶时,写出Y的所有可能值,并估计Y大于零的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com