
分析 画出图形,利用已知条件求出A,B的坐标,通过向量关系求出m值即可.
解答 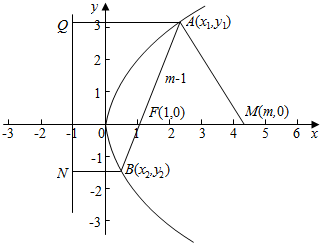 解:由题意可知:F(1,0),由抛物线定义可知A(x1,y1),
解:由题意可知:F(1,0),由抛物线定义可知A(x1,y1),
可知B(x2,y2),
∵$\overrightarrow{AF}$=2$\overrightarrow{FB}$,可得:2(x2-1,y2)=(1-x1,-y1),
可得y2=-$\frac{{y}_{1}}{2}$,x2=$\frac{3-{x}_{1}}{2}$,
$\left\{\begin{array}{l}{{y}_{1}}^{2}=4{x}_{1}\\(-\frac{{y}_{1}}{2})^{2}=4×\frac{3-{x}_{1}}{2}\end{array}\right.$,
解得x1=2,y1=±2$\sqrt{2}$.
|$\overrightarrow{MF}$|=|$\overrightarrow{MA}$|,
可得|m-1|=$\sqrt{({m-2)}^{2}+({0±2\sqrt{2})}^{2}}$,
解得m=$\frac{11}{2}$.
故答案为:$\frac{11}{2}$.
点评 本题考查直线与抛物线方程的综合应用,考查分析问题解决问题的能力.


科目:高中数学 来源: 题型:填空题
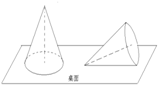 用一个半径为10厘米的半圆纸片卷成一个最大的无底圆锥,放在水平桌面上,被一阵风吹倒,如图,则它的最高点到桌面的距离为5$\sqrt{3}$cm.
用一个半径为10厘米的半圆纸片卷成一个最大的无底圆锥,放在水平桌面上,被一阵风吹倒,如图,则它的最高点到桌面的距离为5$\sqrt{3}$cm.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
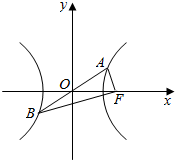 如图,已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)上有一点A,它关于原点的对称点为B,点F为是双曲线的右焦点,且满足AF⊥BF,设∠ABF=α,α∈[$\frac{π}{12}$,$\frac{π}{6}$],则该双曲线离心率e的取值范围为[$\sqrt{2}$,$\sqrt{3}$+1].
如图,已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)上有一点A,它关于原点的对称点为B,点F为是双曲线的右焦点,且满足AF⊥BF,设∠ABF=α,α∈[$\frac{π}{12}$,$\frac{π}{6}$],则该双曲线离心率e的取值范围为[$\sqrt{2}$,$\sqrt{3}$+1].查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(0,-\frac{{\sqrt{6}}}{6}),(0,\frac{{\sqrt{6}}}{6})$ | B. | $(-\frac{{\sqrt{6}}}{6},0),(\frac{{\sqrt{6}}}{6},0)$ | C. | (-1,0),(1,0) | D. | (0,-1)、(0,1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com