
(本小题满分13分)
(本小题满分12分)某地方政府准备在一块面积足够大的荒地上建一如图所示的一个矩形综合性休闲广场,其总面积为3000平方米,其中场地四周(阴影部分)为通道,通道宽度均为2米,中间的三个矩形区域将铺设塑胶地面作为运动场地(其中两个小场地形状相同),塑胶运动场地占地面积为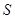 平方米.
平方米.
(1)分别写出用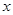 表示
表示 和用
和用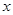 表示
表示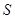 的函数关系式(写出函数定义域);
的函数关系式(写出函数定义域);
(2)怎样设计能使S取得最大值,最大值为多少?
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:解答题
(本小题满分10分)
已知关于x的方程x2+(m-3)x+m=0
(1)若此方程有实数根,求实数m的取值范围.
(2)若此方程的两实数根之差的绝对值小于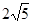 ,求实数m的取值范围.
,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)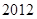 年中秋、国庆长假期间,由于国家实行
年中秋、国庆长假期间,由于国家实行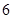 座及以下小型车辆高速公路免费政策,导致在长假期间高速公路出现拥堵现象。长假过后,据有关数据显示,某高速收费路口从上午
座及以下小型车辆高速公路免费政策,导致在长假期间高速公路出现拥堵现象。长假过后,据有关数据显示,某高速收费路口从上午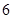 点到中午
点到中午 点,车辆通过该收费站的用时
点,车辆通过该收费站的用时 (分钟)与车辆到达该收费站的时刻
(分钟)与车辆到达该收费站的时刻 之间的函数关系式可近似地用以下函数给出:
之间的函数关系式可近似地用以下函数给出:
y=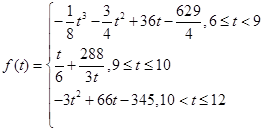
求从上午 点到中午
点到中午 点,通过该收费站用时最多的时刻。
点,通过该收费站用时最多的时刻。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分) 某工厂每天生产某种产品最多不超过40件,并且在生产过程中产品的正品率P与每日生产产品件数x(x∈N*)间的关系为P=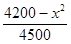 ,每生产一件正品盈利4000元,每出现一件次品亏损2000元.(注:正品率=产品的正品件数÷产品总件数×100%).
,每生产一件正品盈利4000元,每出现一件次品亏损2000元.(注:正品率=产品的正品件数÷产品总件数×100%).
(Ⅰ)将日利润y(元)表示成日产量x(件)的函数;
(Ⅱ)求该厂的日产量为多少件时,日利润最大?并求出日利润的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分15分)
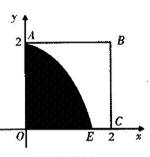
如图,某小区有一边长为2(单位:百米)的正方形地块OABC,其中OAE是一个游泳池,计划在地块OABC内修一条与池边AE相切的直路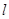 (宽度不计),切点为M,并把该地块分为两部分.现以点O为坐标原点,以线段OC所在直线为x轴,建立平面直角坐标系,若池边AE满足函数
(宽度不计),切点为M,并把该地块分为两部分.现以点O为坐标原点,以线段OC所在直线为x轴,建立平面直角坐标系,若池边AE满足函数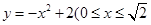 )的图象,且点M到边OA距离为
)的图象,且点M到边OA距离为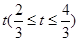 .
.
(1)当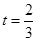 时,求直路
时,求直路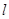 所在的直线方程;
所在的直线方程;
(2)当t为何值时,地块OABC在直路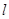 不含泳池那侧的面积取到最大,最大值是多少?
不含泳池那侧的面积取到最大,最大值是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知二次函数y=f1(x)的图象以原点为顶点且过点(1,1),反比例函数y=f2(x)的图象与直线y=x的两个交点间距离为8,f(x)= f1(x)+ f2(x).
(Ⅰ) 求函数f(x)的表达式;
(Ⅱ) 证明:当a>3时,关于x的方程f(x)= f(a)有三个实数解.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)某企业投入81万元经销某产品,经销时间共60个月,市场调研表明,该企业在经销这个产品期间第 个月的利润
个月的利润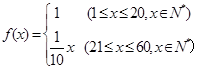 (单位:万元),为了获得更多的利润,企业将每月获得的利润投入到次月的经营中,记第
(单位:万元),为了获得更多的利润,企业将每月获得的利润投入到次月的经营中,记第 个月的当月利润率
个月的当月利润率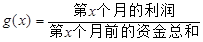 ,例如:
,例如: .
.
(Ⅰ) 求
求 ; (Ⅱ)求第
; (Ⅱ)求第 个月的当月利润率
个月的当月利润率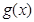 ;
;
(Ⅲ)该企业经销此产品期间,哪个月的当月利润率最大,并求该月的当月利润率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com