已知函数
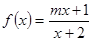
(1)若
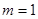
,判断函数
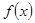
在
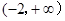
上的单调性并用定义证明;
(2)若函数
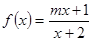
在
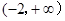
上是增函数,求实数
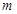
的取值范围.
试题分析: (1)由分离常数法判断函数
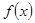
的单调性,由定义法来证明
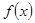
在
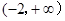
上的单调性注意通分后分解因式,判定各因式的符号.
(2)设
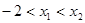
由
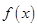
增函数知
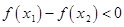
,然后分解因式判定含有
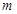
因式的符号
试题解析: (1)当
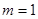
时,

, 1分
设
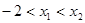
,则
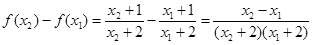
3分
∵
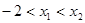
∴
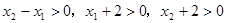
,
∴
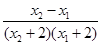
>0, 5分
即
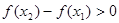
,∴函数
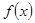
在
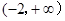
上是增函数. 6分
(2)设
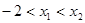
,由
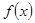
在
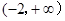
上是增函数,有
即
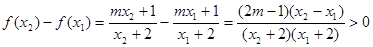
成立, 8分
∵
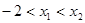
,∴
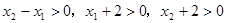
,
必须
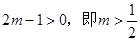
11分
所以,实数
的取值范围是
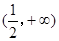
12分
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
已知奇函数
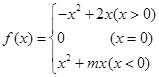
(1)求实数
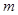
的值,并在给出的直角坐标系中画出
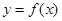
的图象;
(2)若函数
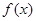
在区间
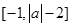
上单调递增,试确定实数
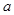
的取值范围.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
设
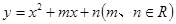
,当
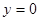
时,对应
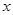
值的集合为
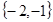
.
(1)求
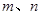
的值;(2)若
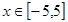
,求该函数的最值.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
设函数
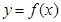
的定义域为
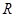
,并且满足
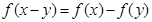
,且
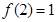
,当
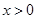
时,
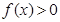
(1).求
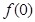
的值;(3分)
(2).判断函数
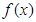
的奇偶性;(3分)
(3).如果
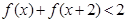
,求
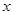
的取值范围.(6分)
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
若函数
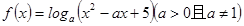
满足对任意的
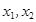
,当
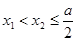
时
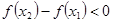
,则实数
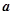
的取值范围是( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
设函数
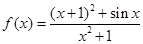
的最大值为
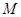
,最小值为
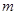
,则
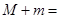
__________.
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
设
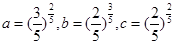
,则a,b,c的大小关系是 ( )
| A.a>c>b | B.a>b>c | C.c>a>b | D.b>c>a |
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
已知
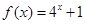
,
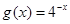
,若偶函数
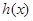
满足
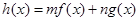
(其中m,n为常数),且最小值为1,则
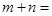
.
查看答案和解析>>

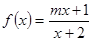
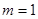 ,判断函数
,判断函数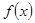 在
在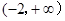 上的单调性并用定义证明;
上的单调性并用定义证明;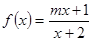 在
在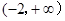 上是增函数,求实数
上是增函数,求实数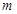 的取值范围.
的取值范围. 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案