
����Ŀ��������������ֱ��������ͽ�Լ��Դ������ƽ���̬�������衣���в������²�ר��100����Ԫ���ֱ�����ֲ�̻��̺ʹ�����Ⱦ������̬ά����Ŀ��ֲ�̻�����Ŀ�����ڴ�������̬����ɱ�ʾΪͶ���ʽ�![]() (��λ������Ԫ)�ĺ���
(��λ������Ԫ)�ĺ���![]() (��λ������Ԫ)��
(��λ������Ԫ)��![]() ��������Ⱦ��Ŀ�����ڴ�������̬����ɱ�ʾΪͶ���ʽ�
��������Ⱦ��Ŀ�����ڴ�������̬����ɱ�ʾΪͶ���ʽ�![]() ��λ��(��λ������Ԫ)�ĺ���
��λ��(��λ������Ԫ)�ĺ���![]() (��λ������Ԫ)��
(��λ������Ԫ)��![]() ��
��
(1)������ֲ�̻�����Ŀ���ʽ�Ϊ![]() (����Ԫ)����������̬��Ŀ�����ڴ����������ܺ�Ϊy��д��y����
(����Ԫ)����������̬��Ŀ�����ڴ����������ܺ�Ϊy��д��y����![]() �ĺ�������ʽ�Ͷ�����
�ĺ�������ʽ�Ͷ�����
(2)�����y�����ֵ���������ʱ��������̬��Ŀ��Ͷ�ʷֱ�Ϊ���٣�
���𰸡���1��![]() ��
��![]() ����2��y�����ֵΪ52����Ԫ���ֱ�Ͷ�ʸ�ֲ�̻�����Ŀ����Ⱦ������Ŀ���ʽ�Ϊ40����Ԫ��60����Ԫ.
����2��y�����ֵΪ52����Ԫ���ֱ�Ͷ�ʸ�ֲ�̻�����Ŀ����Ⱦ������Ŀ���ʽ�Ϊ40����Ԫ��60����Ԫ.
��������
(1) ������ɵô�����Ⱦ��ĿͶ���ʽ�Ϊ![]() ����Ԫ���ɴ˿ɵ�
����Ԫ���ɴ˿ɵ�![]() ,�ٽ�
,�ٽ�![]() ��
��![]() ��ӿɵ�
��ӿɵ�![]() .
.
(2)��![]() ���κ����û�������ʽ�ɵ����ֵ�Լ�ȡ�����ֵ������.
���κ����û�������ʽ�ɵ����ֵ�Լ�ȡ�����ֵ������.
��:��1��������ɵô�����Ⱦ��ĿͶ���ʽ�Ϊ![]() ����Ԫ��
����Ԫ��
����![]() ��
��
��![]()
![]()
![]() ��
��![]() ��
��
����![]() ��
��![]() .
.
��2���ɣ�1����![]()
![]()
![]()
���ҽ���![]() ����
����![]() ʱ�Ⱥų�����
ʱ�Ⱥų�����
��ʱ![]() .
.
��y�����ֵΪ52����Ԫ���ֱ�Ͷ�ʸ�ֲ�̻�����Ŀ����Ⱦ������Ŀ���ʽ�Ϊ40����Ԫ��60����Ԫ��


 ���ĺ����Ͼ�������ϵ�д�
���ĺ����Ͼ�������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һƬɭ��ԭ���Ϊ![]() ���ƻ���ij�꿪ʼ��ÿ�꿳��һЩ���֣���ÿ�꿳���������һ��ʣ������İٷֱ����.���ƻ�������ԭ�����һ��ʱ������ʱ����10��.Ϊ������̬������ɭ���������Ҫ����ԭ�����
���ƻ���ij�꿪ʼ��ÿ�꿳��һЩ���֣���ÿ�꿳���������һ��ʣ������İٷֱ����.���ƻ�������ԭ�����һ��ʱ������ʱ����10��.Ϊ������̬������ɭ���������Ҫ����ԭ�����![]() .��֪������Ϊֹ��ɭ��ʣ�����Ϊԭ�����
.��֪������Ϊֹ��ɭ��ʣ�����Ϊԭ�����![]() .
.
��1����ÿ�꿳���������һ��ʣ������İٷֱȣ�
��2��������Ϊֹ����ɭ���ѿ����˶����ꣿ
��3��Ϊ������̬������������ܿ��������ꣿ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ڶ�����![]() �ϵĺ���
�ϵĺ���![]() ��������ʵ��
��������ʵ��![]() ��
��![]() ��
��![]() ��
��![]() ��ʹ�ö�������
��ʹ�ö�������![]() ����
����![]() ��������ƺ���
��������ƺ���![]() �Ǵ�״��������
�Ǵ�״��������![]() ������Сֵ
������Сֵ![]() �����
�����![]() ����.
����.
��1���жϺ���![]() �Dz��Ǵ�״����������ǣ�ָ������������֤������������ǣ���˵�����ɣ�
�Dz��Ǵ�״����������ǣ�ָ������������֤������������ǣ���˵�����ɣ�
��2����֤������![]() ��
��![]() ���Ǵ�״������
���Ǵ�״������
��3����֤������![]() �Ǵ�״�����ij�Ҫ������
�Ǵ�״�����ij�Ҫ������![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AOB��һ��뾶Ϊr�����οյأ�![]() ��ij��λ�ƻ��ڿյ�����һ�����εĻ����OCDE��һ����ͣ����EFGH��ʣ��ĵط������̻�����
��ij��λ�ƻ��ڿյ�����һ�����εĻ����OCDE��һ����ͣ����EFGH��ʣ��ĵط������̻�����![]() ����
����![]()
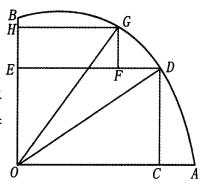
(��)�ǻ������ͣ����ռ�������Ϊ![]() ����
����![]() �ı���ʽ��
�ı���ʽ��
(��)��![]() Ϊ��ֵʱ����ʹ�������ͣ����ռ����������
Ϊ��ֵʱ����ʹ�������ͣ����ռ����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ����ÿ���㶼�Ժ졢����ɫ֮һ��ɫ��֤���������������������������Σ����ǵ����Ʊ�Ϊ1995������ÿһ�������ε���������ͬɫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��x��[��1,1]������
��x��[��1,1]������![]() ,a��R����СֵΪh��a��.
,a��R����СֵΪh��a��.
��1����h��a���Ľ���ʽ��
��2���Ƿ����ʵ��m��nͬʱ��������������������m>n>3���ڵ�h��a���Ķ�����Ϊ[n��m]ʱ��ֵ��Ϊ[n2��m2]�������ڣ����m��n��ֵ���������ڣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() ������
������![]() �ϵ�ֵ��
�ϵ�ֵ��![]() .
.
(1)��![]() ��ֵ��
��ֵ��
(2)������ʽ![]() ��
��![]() �Ϻ��������ʵ��
�Ϻ��������ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
(3)������![]() ��������㣬��ʵ��
��������㣬��ʵ��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���f��x����������f��0����1����f��x+1����f��x����2x��
��1������f��x���Ľ���ʽ��
��2��������[��1��1]�ϣ�y��f��x����ͼ�����y��2x+m��ͼ���Ϸ�����ȷ��ʵ��m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�����⣺������![]() ��ͼ����ڵ�
��ͼ����ڵ�![]() �����ĶԳ�ͼ�Ρ��ĵȼ�����Ϊ������
�����ĶԳ�ͼ�Ρ��ĵȼ�����Ϊ������![]() ���溯����.
���溯����.
��1��������![]() ��ͼ������ƽ��1����λ��������ƽ��2����λ�����ʱͼ���Ӧ�ĺ�������ʽ�������������е�����������
��ͼ������ƽ��1����λ��������ƽ��2����λ�����ʱͼ���Ӧ�ĺ�������ʽ�������������е�����������![]() ͼ��Գ����ĵ����ꣻ
ͼ��Գ����ĵ����ꣻ
��2����֪���⣺������![]() ��ͼ�����ijֱ�߳���Գ�ͼ�ĵȼ�����Ϊ������ʵ��a��b��ʹ�ú���
��ͼ�����ijֱ�߳���Գ�ͼ�ĵȼ�����Ϊ������ʵ��a��b��ʹ�ú���![]() ��ż������.�ϸ���������.����������⣬�����֤��������Ǽ����⣬��˵�����ɣ�������������������������ģ�ʹ֮��Ϊ�����⣨����֤����.
��ż������.�ϸ���������.����������⣬�����֤��������Ǽ����⣬��˵�����ɣ�������������������������ģ�ʹ֮��Ϊ�����⣨����֤����.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com