
分析 (1)利用正弦定理化简已知等式,再由余弦定理列出关系式,将得出的等式变形后代入求出cosA的值,利用特殊角的三角函数值即可求出A的度数.
(Ⅱ)由(Ⅰ)结合基本不等式可得bc≤2+$\sqrt{3}$,再根据面积公式即可求出答案.
解答 解:(Ⅰ)利用正弦定理化简csinC-asinA=($\sqrt{3}$c-b)sinB.
得:c2+b2-$\sqrt{3}$bc=a2,
即c2+b2-a2=$\sqrt{3}$bc,
∴由余弦定理可得:cosA=$\frac{{c}^{2}+{b}^{2}-{a}^{2}}{2bc}$=$\frac{\sqrt{3}bc}{2bc}$=$\frac{\sqrt{3}}{2}$
∵A为三角形内角,
∴A=30°.
(Ⅱ)由(1)可得c2+b2-1=$\sqrt{3}$bc,
∴2bc-1≤$\sqrt{3}$bc,当且仅当b=c时取等号,
∴bc≤$\frac{1}{2-\sqrt{3}}$=2+$\sqrt{3}$
∴S△ABC=$\frac{1}{2}$bcsinA=$\frac{1}{4}$bc≤$\frac{2+\sqrt{3}}{4}$
∴三角形ABC面积S的最大值$\frac{2+\sqrt{3}}{4}$.
点评 此题考查了余弦定理,正弦定理,三角形面积公式的应用,基本不等式,考查了三角函数中的恒等变换应用,熟练掌握定理是解本题的关键.


 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:高中数学 来源: 题型:选择题
| A. | -7 | B. | -3 | C. | 3 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
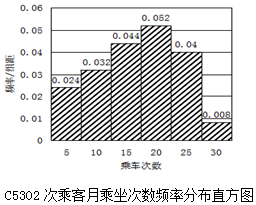 孝汉城铁于12月1日开通,C5302、C5321两列车乘务组工作人员为了了解乘坐本次列车的乘客每月需求情况,分别在两个车次各随机抽取了100名旅客进行调查,下面是根据调查结果,绘制了乘车次数的频率分布直方图和频数分布表.
孝汉城铁于12月1日开通,C5302、C5321两列车乘务组工作人员为了了解乘坐本次列车的乘客每月需求情况,分别在两个车次各随机抽取了100名旅客进行调查,下面是根据调查结果,绘制了乘车次数的频率分布直方图和频数分布表.| 乘车次数分组 | 频数 |
| [0,5) | 15 |
| [5,10) | 20 |
| [10,15) | 25 |
| [15,20) | 24 |
| [20,25) | 11 |
| [25,30] | 5 |
| 老乘客 | 新乘客 | 合计 | |
| 50岁以上 | 10 | 25 | 35 |
| 50岁以下 | 30 | 35 | 65 |
| 合计 | 40 | 60 | 100 |
| P(k2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{5}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {4,5} | B. | {2,3} | C. | {1} | D. | {4} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com