
【题目】已知函数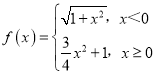 ,点
,点![]() 是函数
是函数![]() 图象上不同的两点,则
图象上不同的两点,则![]() 为坐标原点)的取值范围是( )
为坐标原点)的取值范围是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
【答案】A
【解析】
根据分段函数的表达式,分别求出对应切线和双曲线渐近线的倾斜角,结合位置关系判断∠AOB的大小即可.
当x<0时,y=![]() ,则y2=1+x2,当
,则y2=1+x2,当![]() 时,
时,![]() ,作出函数图象:
,作出函数图象:

当x<0时,y=![]() ,则y2=1+x2,
,则y2=1+x2,
即![]() ,为双曲线在第二象限的一部分,
,为双曲线在第二象限的一部分,
双曲线的渐近线方程为![]() ,
,
若B在双曲线上,则∠BOy的范围是0<∠BOy<![]() ,
,
设当x≥0时,过原点的切线与f(x)=![]() x2+1,相切,
x2+1,相切,
设切点为![]() ,
,
则f′(x)=![]() x,即切线斜率k=
x,即切线斜率k=![]() a,
a,
则切线方程为![]() ,
,
∵切线过原点,
∴![]() ,
,
即![]() ,
,
得![]()
![]() =1,即
=1,即![]() =
=![]() ,则
,则![]() =
=![]() ,
,
则切线斜率![]() ,即切线倾斜角为
,即切线倾斜角为![]() ,
,
则∠AOy的最大值为![]() ,
,
即0≤∠AOy≤![]() ,
,
则0<∠AOy+∠BOy<![]() ,
,
即0<∠AOB<![]() ,
,
故选:A.


 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,以坐标原点为极点,
中,以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() 经过点
经过点![]() 且倾斜角为
且倾斜角为![]() .
.
(1)求曲线![]() 的极坐标方程和直线
的极坐标方程和直线![]() 的参数方程;
的参数方程;
(2)已知直线![]() 与曲线
与曲线![]() 交于
交于![]() ,满足
,满足![]() 为
为![]() 的中点,求
的中点,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 为多面体,平面
为多面体,平面![]() 与平面
与平面![]() 垂直,点
垂直,点![]() 在线段
在线段![]() 上,
上,![]()
![]() 都是正三角形.
都是正三角形.

(1)证明:直线![]() ∥面
∥面![]() ;
;
(2)在线段![]() 上是否存在一点
上是否存在一点![]() ,使得二面角
,使得二面角![]() 的余弦值是
的余弦值是![]() ,若不存在请说明理由,若存在请求出
,若不存在请说明理由,若存在请求出![]() 点所在的位置。
点所在的位置。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】全国大学生机器人大赛是由共青团中央,全国学联,深圳市人民政府联合主办的赛事,是中国最具影响力的机器人项目,是全球独创的机器人竞技平台.全国大学生机器人大赛比拼的是参赛选手们的能力,坚持和态度,展现的是个人实力以及整个团队的力量.2015赛季共吸引全国240余支机器人战队踊跃报名,这些参赛战队来自全国六大赛区,150余所高等院校,其中不乏北京大学,清华大学,上海交大,中国科大,西安交大等众多国内顶尖高校,经过严格筛选,最终由111支机器人战队参与到2015年全国大学生机器人大赛的激烈角逐之中,某大学共有“机器人”兴趣团队1000个,大一、大二、大三、大四分别有100,200,300,400个,为挑选优秀团队,现用分层抽样的方法,从以上团队中抽取20个团队.
(1)应从大三抽取多少个团队?
(2)将20个团队分为甲、乙两组,每组10个团队,进行理论和实践操作考试(共150分),甲、乙两组的分数如下:
甲:125,141,140,137,122,114,119,139,121,142
乙:127,116,144,127,144,116,140,140,116,140
从甲、乙两组中选一组强化训练,备战机器人大赛.
(i)从统计学数据看,若选择甲组,理由是什么?若选择乙组,理由是什么?
(ii)从乙组中不低于140分的团队中任取两个团队,求至少有一个团队为144分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直角梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点,沿
的中点,沿![]() 将
将![]() 折起,使得点
折起,使得点![]() 到点
到点![]() 位置,且
位置,且![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() 是
是![]() 上的动点(与点
上的动点(与点![]() ,
,![]() 不重合).
不重合).
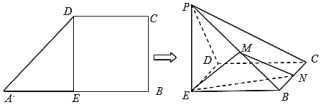
(Ⅰ)证明:平面![]() 平面
平面![]() 垂直;
垂直;
(Ⅱ)是否存在点![]() ,使得二面角
,使得二面角![]() 的余弦值
的余弦值![]() ?若存在,确定
?若存在,确定![]() 点位置;若不存在,说明理由.
点位置;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某歌手大赛进行电视直播,比赛现场有6名特约嘉宾给每位参赛选手评分,场内外的观众可以通过网络平台给每位参赛选手评分.某选手参加比赛后,现场嘉宾评分情况如下表;场内外共有数万名观众参与了评分,组织方将观众评分按照![]() ,
,![]() ,
,![]() 分组,绘成频率分布直方图如下:
分组,绘成频率分布直方图如下:
嘉宾 |
|
|
|
|
|
|
评分 | 96 | 95 | 96 | 89 | 97 | 98 |
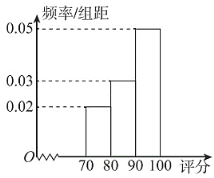
(1)从观众中任取三人,求这三人中恰有1人分数在![]() 另2人分数在
另2人分数在![]() 的概率;
的概率;
(2)从嘉宾中随机选3人,记3人中分数不低于96分的人数为![]() ,求
,求![]() 的期望;
的期望;
(3)嘉宾评分的平均数为![]() ,场内外的观众评分的平均数为
,场内外的观众评分的平均数为![]() 与
与![]() 的大小关系(不需要证明).
的大小关系(不需要证明).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】维生素C又叫抗坏血酸,是一种水溶性维生素,是高等灵长类动物与其他少数生物的必需营养素.维生素C虽不直接构成脑组织,也不向脑提供活动能源,但维生素C有多种健脑强身的功效,它是脑功能极为重要的营养物.维生素C的毒性很小,但食用过多仍可产生一些不良反应.根据食物中维C的含量可大致分为:含量很丰富:鲜枣、沙棘、猕猴桃、柚子,每100克中的维生素C含量超过100毫克;比较丰富:青椒、桂圆、番茄、草莓、甘蓝、黄瓜、柑橘、菜花,每100克中维生素C含量超过50毫克;相对丰富:白菜、油菜、香菜、菠菜、芹菜、苋菜、菜苔、豌豆、豇豆、萝卜,每100克中维生素C含量超过30~50毫克.现从猕猴桃、柚子两种食物中测得每100克所含维生素C的量(单位:![]() )得到茎叶图如图所示,则下列说法中不正确的是( )
)得到茎叶图如图所示,则下列说法中不正确的是( )
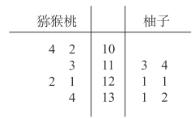
A.猕猴桃的平均数小于柚子的平均数
B.猕猴桃的方差小于柚子的方差
C.猕猴桃的极差为32
D.柚子的中位数为121
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com