【题目】已知△ABC的三个顶点A（﹣1，0），B（1，0），C（3，2），其外接圆为⊙H．若直线l过点C，且被⊙H截得的弦长为2，求直线l的方程．
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=cos2x﹣sinxcosx
（1）求f（x）的最小正周期；
（2）求函数f（x）的单调递增区间；
（3）求f（x）在区间 
上的最大值和最小值．
查看答案和解析>>
科目：高中数学 来源： 题型：
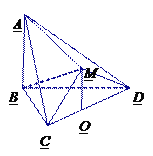
【题目】如图，在多面体
中，△
是等边三角形，△
是等腰直角三角形， 
，平面
平面
， 
平面
，点
为
的中点，连接
.
(1) 求证： 
∥平面
；
(2)若
，求三棱锥
的体积.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】2016年奥运会于8月5日在巴西里约热内卢举行，为了解某单位员工对奥运会的关注情况，对本单位部分员工进行了调查，得到平均每天看奥运会直播时间的茎叶图如下（单位：分钟），若平均每天看奥运会直播不低于70分钟的员工可以视为“关注奥运”，否则视为“不关注奥运”.
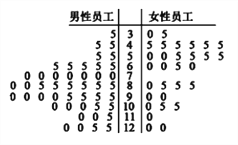
（1）试完成下面表格，并根据此数据判断是否有99.5%以上的把握认为是否“关注奥运会”与性别有关？
（2）若从参与调查且平均每天观看奥运会时间不低于110分钟的员工中抽取4人，用
表示抽取的女员工数，求
的分布列和期望值.
参考公式：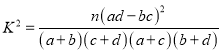 
，其中
| 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=|x﹣a|，g（x）=ax，（a∈R）．
（1）若函数y=f（x）是偶函数，求出符合条件的实数a的值；
（2）若方程f（x）=g（x）有两解，求出实数a的取值范围；
（3）若a＞0，记F（x）=g（x）f（x），试求函数y=F（x）在区间[1，2]上的最大值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在如图所示的几何体中，四边形ABCD是等腰梯形，AB∥CD，∠DAB=60°，FC⊥平面ABCD，AE⊥BD，CB=CD=CF．
（Ⅰ）求证：BD⊥平面AED；
（Ⅱ）求二面角F﹣BD﹣C的余弦值．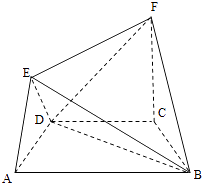
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设数列{an}前n项和为Sn ， 且Sn+an=2． （Ⅰ）求数列{an}的通项公式；
（Ⅱ）若数列{bn}满足b1=a1 ， bn= 
，n≥2 求证{ 
}为等比数列，并求数列{bn}的通项公式；
（Ⅲ）设cn= 
，求数列{cn}的前n和Tn ．
查看答案和解析>>
科目：高中数学 来源： 题型：
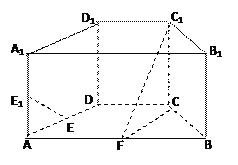
【题目】如图，在直四棱柱ABCD-A
BCD中，底面ABCD为等腰梯形，AB//CD，AB=4, BC=CD=2, AA=2, E、E、F分别是棱AD、AA、AB的中点。
证明：（1）直线EE//平面FCC；
（2）求二面角B-FC-C的余弦值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
