分析:(1)函数的解析式知,自变量x要满足cos2x≠0,由此即可解出定义域,求函数的值域要先对函数的解析式进行化简,解析式可变为f(x)=4sin(2x+
)-2由三角函数的有界性易得函数的最值;
(2)由(1)得f(x)=4sin(2x+
)-2,求此函数的单调性增区间,令相位2x+
∈[2kπ-
,2kπ+
],从中解出x的取值范围,即为函数的单调增区间.
解答:解:(1)由f(x)=
-4sin
2x,x要满足cos2x≠0,从而2x≠kπ+
(k∈Z)
因此f(x)的定义域为{x|x≠
kπ+
,(k∈Z)}
又f(x)=2
sin2x-2(2sin
2x-1)-2=2
sin2x+cos2x-2=4sin(2x+
)-2
∴-6≤f(x)≤2,当2x+
=2kπ+
,有f(x)=2
∴x=kπ+
,k∈Z时,f(x)的最大值为2
(2)由f(x)=4sin(2x+
)-2,2x≠2kπ±
由2kπ-
≤2x+
≤2kπ+
可知:
kπ-
≤x≤kπ+
且x≠kπ-
于是f(x)在[kπ-
,kπ-
)上为增函数,在(kπ-
,kπ+
]上也是增函数.
点评:本题考查了二倍角的正弦、余弦公式,正弦的和角公式,三角函数最值的求法,综合性较强,解题的关键是熟练掌握三角函数中的有关公式且能根据这些公式灵活变形,本题第二小题易出错易因为忘记函数的定义域而出错,做题是要前后结合,完成题目后要复查一遍,另外,有着严密的逻辑推理习惯也有助于此类题的正确解答



 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案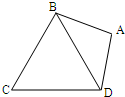 (2007•武汉模拟)如图,在平面四边形ABCD中,AB=AD=1,∠BAD=θ,而△BCD是正三角形,
(2007•武汉模拟)如图,在平面四边形ABCD中,AB=AD=1,∠BAD=θ,而△BCD是正三角形, (2007•武汉模拟)如图,直线l:y=
(2007•武汉模拟)如图,直线l:y=