Question

15．以下命题中：
①命题：“?x∈R，f（x）g（x）=0”的否定是“?x₀∈R，f（x₀）g（x₀）≠0”；
②点P是抛物线y²=2x上的动点，点M是P在y轴上的射影，点A的坐标是A（3，6），则|PA|+|PM|的最小值是6；
③命题“若P则q”与命题“若非p则非q”互为逆否命题；
④若过点C（1，1）的直线l交椭圆C：$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1于不同的两点A，B，且C是AB的中点，则直线l的方程是3x+4y-7=0．
其中真命题的序号是①②④．（写出所有真命题的序号）

Answer 1

分析 对于①，写出命题：“?x∈R，f（x）g（x）=0”的否定，即可判断①的正误；
对于②，依题意，作出图形，利用抛物线的定义，可知|PA|+|PM|=|PA|+|PN|-$\frac{1}{2}$=|PA|+|PF|-$\frac{1}{2}$≥|AF|-$\frac{1}{2}$，即可判断②的正误；
对于③，写出命题“若P则q”的逆否命题，即可判断③的正误；
对于④，设A（x₁，y₁），B（x₂，y₂），则$\frac{{{x}_{1}}^{2}}{4}$+$\frac{{{y}_{1}}^{2}}{3}$=1，$\frac{{{x}_{2}}^{2}}{4}$+$\frac{{{y}_{2}}^{2}}{3}$=1，两式相减，结合C（1，1）是AB的中点，可得：k_AB=-$\frac{3}{4}$，从而可求得直线AB的方程，又即可判断④的正误．

解答 解：对于①，命题：“?x∈R，f（x）g（x）=0”的否定是“?x₀∈R，f（x₀）g（x₀）≠0”，故①正确；
对于②，点P是抛物线y²=2x上的动点，点M是P在y轴上的射影，点A的坐标是A（3，6），设点P在抛物线的准线x=-$\frac{1}{2}$上的射影为N，作图如下：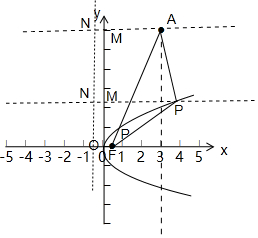

由抛物线的定义知，|PN|=|PF|，故|PM|=|PN|-$\frac{1}{2}$，
则|PA|+|PM|=|PA|+|PN|-$\frac{1}{2}$=|PA|+|PF|-$\frac{1}{2}$≥|AF|-$\frac{1}{2}$=$\sqrt{{（3-\frac{1}{2}）}^{2}{+（6-0）}^{2}}$-$\frac{1}{2}$=$\frac{13}{2}$-$\frac{1}{2}$=6，
即|PA|+|PM|的最小值是6，故②正确；
对于③，命题“若p则q”与命题“若非q则非p”互为逆否命题，与命题“若非p则非q”互为否命题，故③错误；
对于④，若过点C（1，1）的直线l交椭圆C：$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1于不同的两点A（x₁，y₁），B（x₂，y₂），
则$\frac{{{x}_{1}}^{2}}{4}$+$\frac{{{y}_{1}}^{2}}{3}$=1，$\frac{{{x}_{2}}^{2}}{4}$+$\frac{{{y}_{2}}^{2}}{3}$=1，
两式相减，整理得：k_AB=-$\frac{3}{4}$•$\frac{{x}_{1}{+x}_{2}}{{y}_{1}{+y}_{2}}$，又C（1，1）是AB的中点，
所以x₁+x₂=2，y₁+y₂=2，
所以k_AB=-$\frac{3}{4}$，
则直线l的方程是3x+4y-7=0，故④正确；
综上所述，其中真命题的序号是①②④，
故答案为：①②④．

点评 本题考查命题的真假判断与应用，突出考查四种命题之间的关系及全称命题与特称命题的转化，考查抛物线定义与“点差法”的综合运用，特别是等价转化思想、数形结合思想的应用，属于难题．