
【题目】已知函数![]() (其中
(其中![]() ,且
,且![]() 为常数).
为常数).
(1)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(2)若对于任意的![]() ,都有
,都有![]() 成立,求
成立,求![]() 的取值范围;
的取值范围;
(3)若方程![]() 在
在![]() 上有且只有一个实根,求
上有且只有一个实根,求![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)在(0,1),![]() 上单调递增,在(1,2)上单调递减(Ⅱ)
上单调递增,在(1,2)上单调递减(Ⅱ)![]() (Ⅲ)
(Ⅲ)![]()
【解析】【试题分析】(1)将![]() 代入
代入![]() 再求导,借助导函数值的符号确定函数
再求导,借助导函数值的符号确定函数![]() 的单调区间;(2)借助问题(1)的结论,对参数
的单调区间;(2)借助问题(1)的结论,对参数![]() 进行分类讨论,最终确定参数
进行分类讨论,最终确定参数![]() 的取值范围;(3)依据题设条件将问题进行等价转化为
的取值范围;(3)依据题设条件将问题进行等价转化为![]() 的零点的个数问题,再运用导数知识及分类整合思想进行分析探求:
的零点的个数问题,再运用导数知识及分类整合思想进行分析探求:
解:⑴函数![]() 的定义域为
的定义域为![]()
由![]() 知
知
当![]() 时,
时,![]()
所以函数![]() 在(0,1)上单调递增,在(1,2)上单调递减,
在(0,1)上单调递增,在(1,2)上单调递减,![]() 在上单调递增
在上单调递增
(Ⅱ)由![]()
当![]() 时,
时,![]() 对于
对于![]() 恒成立,
恒成立,![]() 在
在![]() 上单调递增
上单调递增
![]() ,此时命题成立;
,此时命题成立;
当![]() 时,
时,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增, ![]() 当
当![]() 时,有
时,有![]() .这与题设矛盾,不合. 故
.这与题设矛盾,不合. 故![]() 的取值范围是
的取值范围是![]()
(Ⅲ)依题意,设![]() ,原题即为若
,原题即为若![]() 在
在![]() 上有且只有一个零点,求
上有且只有一个零点,求![]() 的取值范围.显然函数
的取值范围.显然函数![]() 与
与![]() 的单调性是一致的.
的单调性是一致的.
当![]() 时,因为函数
时,因为函数![]() 在
在![]() 上递增,由题意可知
上递增,由题意可知![]() 解得
解得![]() ;
;
当![]() 时,因为
时,因为![]() ,当
,当![]() 时,总有
时,总有![]() ,此时方程没有实根。
,此时方程没有实根。
综上所述,当![]() 时,方程
时,方程![]() 在
在![]() 上有且只有一个实根。
上有且只有一个实根。


科目:高中数学 来源: 题型:
【题目】若二次函数f(x)=x2+bx+c满足f(2)=f(﹣2),且函数的f(x)的一个零点为1. (Ⅰ)求函数f(x)的解析式;
(Ⅱ)对任意的 ![]() ,4m2f(x)+f(x﹣1)≥4﹣4m2恒成立,求实数m的取值范围.
,4m2f(x)+f(x﹣1)≥4﹣4m2恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x+ ![]() (Ⅰ)判断函数的奇偶性,并加以证明;
(Ⅰ)判断函数的奇偶性,并加以证明;
(Ⅱ)用定义证明f(x)在(0,1)上是减函数;
(Ⅲ)函数f(x)在(﹣1,0)上是单调增函数还是单调减函数?(直接写出答案,不要求写证明过程).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系中,以![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数, ![]() ),直线
),直线![]() 的极坐标方程为
的极坐标方程为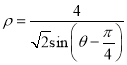 .
.
(1)写出曲线![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)![]() 为曲线
为曲线![]() 上任意一点,
上任意一点, ![]() 为直线
为直线![]() 任意一点,求
任意一点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次国际学术会议上,来自四个国家的五位代表被安排坐在一张圆桌,为了使他们能够自由交谈,事先了解到的情况如下:
甲是中国人,还会说英语.
乙是法国人,还会说日语.
丙是英国人,还会说法语.
丁是日本人,还会说汉语.
戊是法国人,还会说德语.
则这五位代表的座位顺序应为( )
A. 甲丙丁戊乙 B. 甲丁丙乙戊
C. 甲乙丙丁戊 D. 甲丙戊乙丁
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() .
.
(1)若![]() ,讨论函数
,讨论函数![]() 的单调性;
的单调性;
(2)是否存在实数![]() ,对任意
,对任意![]() ,
, ![]() , 有
, 有![]() 恒成立,若存在,求出
恒成立,若存在,求出![]() 的范围,若不存在,请说明理由;
的范围,若不存在,请说明理由;
(3)记![]() ,如果
,如果![]() 是函数
是函数![]() 的两个零点,且
的两个零点,且![]() ,
, ![]() 是
是![]() 的导函数,证明:
的导函数,证明: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=2x+1的定义域为[1,5],则函数f(2x﹣3)的定义域为( )
A.[1,5]
B.[3,11]
C.[3,7]
D.[2,4]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com