
甲、乙、丙、丁4名同学被随机地分到 三个社区参加社会实践,要求每个社区至少有一名同学.
三个社区参加社会实践,要求每个社区至少有一名同学.
(1)求甲、乙两人都被分到 社区的概率;
社区的概率;
(2)求甲、乙两人不在同一个社区的概率;
(3)设随机变量 为四名同学中到
为四名同学中到 社区的人数,求
社区的人数,求 的分布列和
的分布列和 的值.
的值.
(1)甲、乙两人同时到 社区的概率是
社区的概率是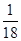 .
.
(2)甲、乙两人不在同一社区的概率是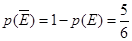 .
.
(3)随机变量 可能取的值为1,2.
可能取的值为1,2. 的分布列是:
的分布列是:
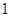

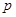
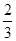
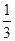
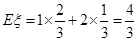 .
.
解析试题分析:(1)由古典概型概率的计算得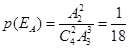 .
.
(2)由古典概型,甲、乙两人在同一社区为事件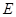 ,那么
,那么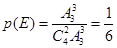 ,根据对立事件的概率公式,甲、乙两人不在同一社区的概率是
,根据对立事件的概率公式,甲、乙两人不在同一社区的概率是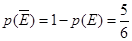 ;
;
(3)随机变量 可能取的值为1,2.事件“
可能取的值为1,2.事件“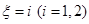 ”是指有
”是指有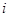 个同学到
个同学到 社区,由古典概型概率的计算即可得到分布列,进一步计算得数学期望.
社区,由古典概型概率的计算即可得到分布列,进一步计算得数学期望.
试题解析:(1)记甲、乙两人同时到 社区为事件
社区为事件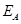 ,那么
,那么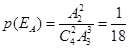 ,
,
即甲、乙两人同时到 社区的概率是
社区的概率是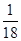 . 2分
. 2分
(2)记甲、乙两人在同一社区为事件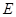 ,那么
,那么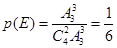 , 4分
, 4分
所以,甲、乙两人不在同一社区的概率是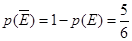 . 6分
. 6分
(3)随机变量 可能取的值为1,2.事件“
可能取的值为1,2.事件“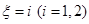 ”是指有
”是指有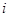 个同学到
个同学到 社区,
社区,
则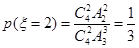 . 8分
. 8分
所以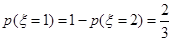 , 10分
, 10分
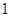

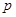
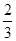
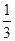
 的分布列是:
的分布列是:
∴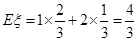 . 12分
. 12分
考点:古典概型,对立事件的概率,离散型随机变量的分布列及数学期望.


科目:高中数学 来源: 题型:解答题
对有 个元素的总体
个元素的总体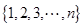 进行抽样,先将总体分成两个子总体
进行抽样,先将总体分成两个子总体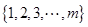 和
和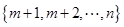 (
(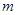 是给定的正整数,且
是给定的正整数,且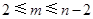 ),再从每个子总体中各随机抽取
),再从每个子总体中各随机抽取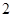 个元素组成样本.用
个元素组成样本.用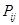 表示元素
表示元素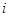 和
和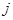 同时出现在样本中的概率.
同时出现在样本中的概率.
(1)求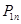 的表达式(用
的表达式(用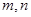 表示);
表示);
(2)求所有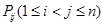 的和.
的和.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某市公租房房屋位于A、B、C三个地区,设每位申请人只申请其中一个片区的房屋,且申请其中任一个片区的房屋是等可能的,求该市的任4位申请人中:
(1)若有2人申请A片区房屋的概率;
(2)申请的房屋在片区的个数的X分布列与期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某商店试销某种商品20天,获得如下数据:
| 日销售量(件) | 0 | 1 | 2 | 3 |
| 频数 | 1 | 5 | 9 | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
生产A,B两种元件,其质量按测试指标划分为:指标大于或等于82为正品,小于82为次品,现随机抽取这两种元件各100件进行检测,检测结果统计如下:
| 测试指标 |  | 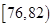 |  |  | 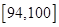 |
| 元件A | 8 | 12 | 40 | 32] | 8 |
| 元件B | 7 | 18 | 40 | 29 | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
一个口袋中有 个白球和
个白球和 个红球(
个红球( ,且
,且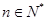 ),每次从袋中摸出两个球(每次摸球后把这两个球放回袋中),若摸出的两个球颜色相同为中奖,否则为不中奖.
),每次从袋中摸出两个球(每次摸球后把这两个球放回袋中),若摸出的两个球颜色相同为中奖,否则为不中奖.
(1)试用含 的代数式表示一次摸球中奖的概率
的代数式表示一次摸球中奖的概率 ;
;
(2)若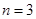 ,求三次摸球恰有一次中奖的概率;
,求三次摸球恰有一次中奖的概率;
(3)记三次摸球恰有一次中奖的概率为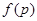 ,当
,当 为何值时,
为何值时,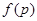 取最大值.
取最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
2014年2月21日,《中共中央关于全面深化改革若干重大问题的决定》明确:坚持计划生育的基本国策,启动实施一方是独生子女的夫妇可生育两个孩子的政策.为了解某地区城镇居民和农村居民对“单独两孩”的看法,某媒体在该地区选择了3600人调查,就是否赞成“单独两孩”的问题,调查统计的结果如下表:
 | 赞成 | 反对 | 无所谓 |
| 农村居民 | 2100人 | 120人 | y人 |
| 城镇居民 | 600人 | x人 | z人 |
 的分布列和数学期望.
的分布列和数学期望.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
生产A,B两种元件,其质量按测试指标划分为:指标大于或等于82为正品,小于82为次品,现随机抽取这两种元件各100件进行检测,检测结果统计如下:
| 测试指标 | [70,76) | [76,82) | [82,88) | [88,94) | [94,100] |
| 元件A | 8 | 12 | 40 | 32 | 8 |
| 元件B | 7 | 18 | 40 | 29 | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
正四面体ABCD的体积为V,P是正四面体ABCD的内部的一个点.
(1)设“VPABC≥ V”的事件为X,求概率P(X);
V”的事件为X,求概率P(X);
(2)设“VPABC≥ V”且“VPBCD≥
V”且“VPBCD≥ V”的事件为Y,求概率P(Y).
V”的事件为Y,求概率P(Y).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com