练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】若a＞b＞1，0＜c＜1，则（ ）
    A.ac＜bc
    B.abc＜bac
    C.alogbc＜blogac
    D.logac＜logbc

    【答案】C
    【解析】解：∵a＞b＞1，0＜c＜1，

    ∴函数f（x）=xc在（0，+∞）上为增函数，故ac＞bc，故A错误；

    函数f（x）=xc﹣1在（0，+∞）上为减函数，故ac﹣1＜bc﹣1，故bac＜abc，即abc＞bac；故B错误；

    logac＜0，且logbc＜0，logab＜1，即 = ＜1，即logac＞logbc．故D错误；

    0＜﹣logac＜﹣logbc，故﹣blogac＜﹣alogbc，即blogac＞alogbc，即alogbc＜blogac，故C正确；

    故选：C

    根据已知中a＞b＞1，0＜c＜1，结合对数函数和幂函数的单调性，分析各个结论的真假，可得答案．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱柱中，平面，，， ，， 为的中点.

    （Ⅰ）求CE与DB所成角的余弦值；

    （Ⅱ）设点在线段上，且直线与平面所成角的正弦值为，求线段的长度

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=ln（x+1）+ ．
    （I）讨论函数f（x）在（0，+∞）上的单调性；
    （II）设函数f（x）存在两个极值点，并记作x1 ， x2 ， 若f（x1）+f（x2）＞4，求正数a的取值范围；
    （III）求证：当a=1时，f（x）＞ （其中e为自然对数的底数）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某地区拟建立一个艺术搏物馆，采取竞标的方式从多家建筑公司选取一家建筑公司，经过层层筛选，甲、乙两家建筑公司进入最后的招标．现从建筑设计院聘请专家设计了一个招标方案：两家公司从6个招标总是中随机抽取3个总题，已知这6个招标问题中，甲公司可正确回答其中4道题目，而乙公司能正面回答每道题目的概率均为 ，甲、乙两家公司对每题的回答都是相独立，互不影响的．
    （1）求甲、乙两家公司共答对2道题目的概率；
    （2）请从期望和方差的角度分析，甲、乙两家哪家公司竞标成功的可能性更大？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知向量 =（m，cos2x）， =（sin2x，n），设函数f（x）= ，且y=f（x）的图象过点（ ， ）和点（ ，﹣2）．
    （Ⅰ）求m，n的值；
    （Ⅱ）将y=f（x）的图象向左平移φ（0＜φ＜π）个单位后得到函数y=g（x）的图象．若y=g（x）的图象上各最高点到点（0，3）的距离的最小值为1，求y=g（x）的单调增区间．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

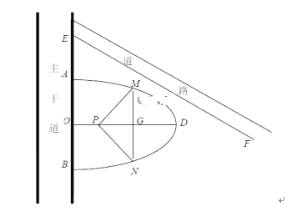
    【题目】某学校决定在主干道旁边挖一个半椭圆形状的小湖，如图所示，AB=4，O为AB的中点，椭圆的焦点P在对称轴OD上，M、N在椭圆上，MN平行AB交OD与G，且G在P的右侧，△MNP为灯光区，用于美化环境.

    (1)若学校的另一条道路EF满足OE=3，tan∠OEF=2，为确保道路安全，要求椭圆上任意一点到道路EF的距离都不小于，求半椭圆形的小湖的最大面积：(椭圆()的面积为)

    (2)若椭圆的离心率为，要求灯光区的周长不小于，求PG的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某保险的基本保费为a（单位：元），继续购买该保险的投保人成为续保人，续保人本年度的保费与其上年度出险次数的关联如下：

    上年度出险次数

    0

    1

    2

    3

    4

    ≥5

    保费

    0.85a

    a

    1.25a

    1.5a

    1.75a

    2a

    设该险种一续保人一年内出险次数与相应概率如下：

    一年内出险次数

    0

    1

    2

    3

    4

    ≥5

    概率

    0.30

    0.15

    0.20

    0.20

    0.10

    0.05

    （Ⅰ）求一续保人本年度的保费高于基本保费的概率；
    （Ⅱ）若一续保人本年度的保费高于基本保费，求其保费比基本保费高出60%的概率；
    （Ⅲ）求续保人本年度的平均保费与基本保费的比值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知双曲线C： ﹣ =1（a＞0，b＞0）的左、右焦点分别为F1 ， F2 ， O为坐标原点，点P是双曲线在第一象限内的点，直线PO，PF2分别交双曲线C的左、右支于另一点M，N，若|PF1|=2|PF2|，且∠MF2N=120°，则双曲线的离心率为（ ）
    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=ex+ax2﹣ex，a∈R．
    （Ⅰ）若曲线y=f（x）在点（1，f（1））处的切线平行于x轴，求函数f（x）的单调区间；
    （Ⅱ）试确定a的取值范围，使得曲线y=f（x）上存在唯一的点P，曲线在该点处的切线与曲线只有一个公共点P．

    查看答案和解析>>

    同步练习册答案