
分析 设出复数x的代数形式,代入原方程列式求出z的实部和虚部,则复数集内方程x2+2|x|-3=0的解可求.
解答 解:设x=a+bi(a,b∈R),
代入x2+2|x|-3=0,得(a+bi)2+2$\sqrt{{a}^{2}+{b}^{2}}$-3=0,
∴a2-b2+2abi+2$\sqrt{{a}^{2}+{b}^{2}}$-3=0,
∴$\left\{\begin{array}{l}{{a}^{2}-{b}^{2}+2\sqrt{{a}^{2}+{b}^{2}}-3=0}\\{2ab=0}\end{array}\right.$,
当a=0时,代入得:-|b|2+2|b|-3=0,b无解
当b=0时,代入得:|a|2+2|a|-3=0,解得|a|=1,a=±1,
∴x=±1.
∴方程的解为±1.
点评 本题考查了复数代数形式的乘除运算,考查了复数相等的条件,是基础的计算题.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案科目:高中数学 来源: 题型:解答题
 如图,四棱锥P-ABCD的底面四边形ABCD是梯形,AB∥CD,M是PC的中点,AM与平面PBD交于点E,且AE=EM.
如图,四棱锥P-ABCD的底面四边形ABCD是梯形,AB∥CD,M是PC的中点,AM与平面PBD交于点E,且AE=EM.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
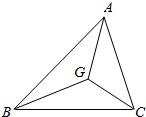 (1)如图,G是△ABC的重心,求证:$\overrightarrow{GA}$+$\overrightarrow{GB}$+$\overrightarrow{GC}$=$\overrightarrow{0}$.
(1)如图,G是△ABC的重心,求证:$\overrightarrow{GA}$+$\overrightarrow{GB}$+$\overrightarrow{GC}$=$\overrightarrow{0}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com