
【题目】如下图,在四棱锥![]() 中,
中,![]() 面
面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点。
的中点。
(1)求证:![]() 面
面![]() ;
;
(2)线段![]() 上是否存在一点
上是否存在一点![]() ,满足
,满足![]() ?若存在,试求出二面角
?若存在,试求出二面角![]() 的余弦值;若不存在,说明理由。
的余弦值;若不存在,说明理由。

【答案】(1)见解析;(2)存在点![]() ,满足
,满足![]() ,二面角
,二面角![]() 的余弦值为
的余弦值为![]() 。
。
【解析】
试题分析:(1)要证![]() 平面
平面![]() ,只要在平面
,只要在平面![]() 内找到一条直线与
内找到一条直线与![]() 平行即可,取
平行即可,取![]() 的中点
的中点![]() ,构造平行四边形
,构造平行四边形![]() 即可证明;(2)以
即可证明;(2)以![]() 分别为
分别为![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() ,写出点
,写出点![]() 的坐标,假设
的坐标,假设![]() 上存在一点
上存在一点![]() 使
使![]() ,利用空间向量知识可得到在
,利用空间向量知识可得到在![]() 上存在点
上存在点![]() 满足条件,平面
满足条件,平面![]() 的一个法向量为
的一个法向量为![]() ,再求出平面
,再求出平面![]() 的法向量,即可求二面角
的法向量,即可求二面角![]() 的余弦值。
的余弦值。
试题解析:(1)取![]() 的中点
的中点![]() ,连
,连![]() 和
和![]() ,过
,过![]() 点作
点作![]() ,垂足为
,垂足为![]()
∵![]() ,
,![]() ,∴
,∴![]() ,又
,又![]()
∴四边形![]() 为平行四边形,
为平行四边形,
∴![]() ,在直角三角形
,在直角三角形![]() 中,
中,
![]()
∴![]() ,而
,而![]() 分别为
分别为![]() 的中点,
的中点,
∴![]() 且
且![]() ,又
,又![]()
∴![]() 且
且![]() ,四边形
,四边形![]() 为平行四边形,
为平行四边形,
∴![]()
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() 。
。
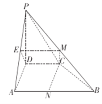
(2)由题意可得,![]() 两两互相垂直,如图,以
两两互相垂直,如图,以![]() 分别为
分别为![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() ,
,
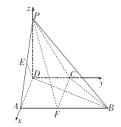
则![]() ,假设
,假设![]() 上存在一点
上存在一点![]() 使
使![]() ,设
,设![]() 坐标为
坐标为![]() ,
,
则![]() ,由
,由![]() ,得
,得![]() ,
,
又平面![]() 的一个法向量为
的一个法向量为![]()
设平面![]() 的法向量为
的法向量为![]()
又![]() ,
,![]() ,
,
由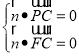 ,得
,得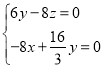 ,即
,即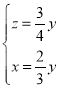
不妨设![]() ,有
,有![]()
则![]()
又由法向量方向知,该二面角为锐二面角,
故二面角![]() 的余弦值为
的余弦值为![]() 。
。


科目:高中数学 来源: 题型:
【题目】设数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() 。
。
(1)求证:数列![]() 为等差数列,并分别写出
为等差数列,并分别写出![]() 和
和![]() 关于
关于![]() 的表达式;
的表达式;
(2)是否存在自然数![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 的值;来若不存在,请说明理由。
的值;来若不存在,请说明理由。
(3)设![]() ,
,![]() ,若不等式
,若不等式![]() 对
对![]() 恒成立,求
恒成立,求![]() 的最大值。
的最大值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】大学毕业生小王相应国家“自主创业”的号召,利用银行小额无息贷款开办了一家饰品店,该店购进一种今年新上市的饰品进行销售,饰品的进价为每件40元,售价为每件60元,每月可卖出300件,市场调查反映:调整价格时,售价每涨1元每月要少卖10件;售价每下降1元每月多卖20件,为获得更大的利润,现将饰品售价调整为![]() (元/件)(
(元/件)(![]() 即售价上涨,
即售价上涨,![]() 即售价下降),每月饰品销售为
即售价下降),每月饰品销售为![]() (件),月利润为
(件),月利润为![]() (元).
(元).
(1)直接写出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)如何确定销售价格才能使月利润最大?求最大月利润;
(3)为了使每月利润不少于6000元,应如何控制销售价格?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对定义在区间![]() 上的函数
上的函数![]() 和
和![]() ,如果对任意
,如果对任意![]() ,都有
,都有![]() 成立,那么称函数
成立,那么称函数![]() 在区间D上可被
在区间D上可被![]() 替代,D称为“替代区间”.给出以下命题:
替代,D称为“替代区间”.给出以下命题:
①![]() 在区间
在区间![]() 上可被
上可被![]() 替代;
替代;
②![]() 可被
可被![]() 替代的一个“替代区间”为
替代的一个“替代区间”为![]() ;
;
③![]() 在区间
在区间![]() 可被
可被![]() 替代,则
替代,则![]() ;
;
④![]() ,则存在实数
,则存在实数![]() ,使得
,使得![]() 在区间
在区间![]() 上被
上被![]() 替代;
替代;
其中真命题的有
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于下列命题:
①若一组数据中的每一个数据都加上同一个数后,方差恒不变;
②满足方程![]() 的
的![]() 值为函数
值为函数![]() 的极值点;
的极值点;
③命题“p且q为真” 是命题“p或q为真”的必要不充分条件;
④若函数![]() (
(![]() 且
且![]() )的反函数的图像过点
)的反函数的图像过点![]() ,则
,则![]() 的最小值为
的最小值为![]() ;
;
⑤点![]() 是曲线
是曲线![]() 上一动点,则
上一动点,则![]() 的最小值是
的最小值是![]() 。
。
其中正确的命题的序号是____________(注:把你认为正确的命题的序号都填上)。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知离心率为![]() 的椭圆
的椭圆![]() ,右焦点到椭圆上的点的距离的最大值为3。
,右焦点到椭圆上的点的距离的最大值为3。

(1)求椭圆![]() 的方程;
的方程;
(2)设点![]() 是椭圆
是椭圆![]() 上两个动点,直线
上两个动点,直线![]() 与椭圆
与椭圆![]() 的另一交点分别为
的另一交点分别为![]() ,且直线
,且直线![]() 的斜率之积等于
的斜率之积等于![]() ,问四边形
,问四边形![]() 的面积
的面积![]() 是否为定值?请说明理由。
是否为定值?请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com