【题目】已知在数列
中， 
， 
， 
.
(1)证明数列
是等差数列，并求
的通项公式；
(2)设数列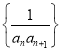
的前
项和为
，证明： 
.
【答案】（1）
（2）见解析
【解析】试题分析：（1）证明一个数列是否为等差数列的基本方法有两种：一是定义法：证明
（
，
为常数；二是等差中项法，证明
，若证明一个数列不是等差数列，则只需举出反例即可；（2）观测数列的特点形式，看使用什么方法求和.使用裂项法求和时，要注意正负项相消时消去了哪些项，保留了哪些项，切不可漏写未被消去的项，未被消去的项有前后对称的特点，实质上造成正负相消是此法的根源和目的.（3）在做题时注意观察式子特点选择有关公式和性质进行化简，这样给做题带来方便，掌握常见求和方法，如分组转化求和，裂项法，错位相减.
试题解析：（1）由
，得
， （2分）
两式相减，得
，即
， （4分）
所以数列
是等差数列. （5分）
由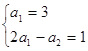
，得
，所以
， （6分）
故
. （8分）
（2）因为
，（11分）
所以
（
） （14分）
科目：高中数学 来源： 题型：
【题目】高考复习经过二轮“见多识广”之后，为了研究考前“限时抢分”强化训练次数
与答题正确率
的关系，对某校高三某班学生进行了关注统计，得到如表数据：
| 1 | 2 | 3 | 4 |
| 20 | 30 | 50 | 60 |
（1）求
关于
的线性回归方程，并预测答题正确率是
的强化训练次数（保留整数）；
（2）若用
（
）表示统计数据的“强化均值”（保留整数），若“强化均值”的标准差在区间
内，则强化训练有效，请问这个班的强化训练是否有效？
附：回归直线的斜率和截距的最小二乘法估计公式分别为：
， 
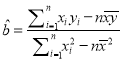，样本数据
， 
，…， 
的标准差为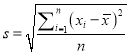
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】从某技术公司开发的某种产品中随机抽取200件，测量这些产品的一项质量指标值(记为
)，由测量结果得到如下频率分布直方图：
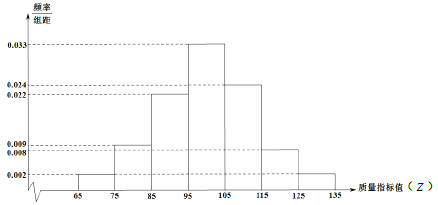
公司规定：当
时，产品为正品；当
时，产品为次品，公司每生产一件这种产品，若是正品，则盈利90元；若是次品，则亏损30元，记
的分布列和数学期望；
由频率分布直方图可以认为，服从正态分布
，其中
近似为样本平均数
，
近似为样本方差
(同一组中的数据用该区间的中点值作代表)
①利用该正态分布，求
；
②某客户从该公司购买了500件这种产品，记
表示这500件产品中该项质量指标值位于区间
的产品件数，利用①的结果，求
.
附：
，
若
，则
，
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】选修4-4：坐标系与参数方程
已知曲线
的参数方程为
（
为参数）.以直角坐标系的原点
为极点，
轴的正半轴为极轴建立坐标系，曲线
的极坐标方程为
.
（1）求的普通方程和的直角坐标方程；
（2）若过点
的直线
与交于
，
两点，与交于
，
两点，求
的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】选修4-4，坐标系与参数方程
已知在平面直角坐标系xOy中，椭圆C的方程为
，以O为极点，x轴的非负半轴为极轴，取相同的长度单位建立极坐标系，直线
的极坐标方程为
．
（1）求直线的直角坐标方程；
（2）设M（x，y）为椭圆C上任意一点，求|
x+y﹣1|的最大值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】选修4-4，坐标系与参数方程
已知在平面直角坐标系xOy中，椭圆C的方程为
，以O为极点，x轴的非负半轴为极轴，取相同的长度单位建立极坐标系，直线
的极坐标方程为
．
（1）求直线的直角坐标方程；
（2）设M（x，y）为椭圆C上任意一点，求|
x+y﹣1|的最大值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
