
【题目】已知函数![]() .
.
(1)求函数![]() 的极值;
的极值;
(2)设函数![]() ,若存在
,若存在![]() ,使
,使![]() ,证明:
,证明:![]() .
.
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案科目:高中数学 来源: 题型:
【题目】圆周上有800个点,依顺时针方向标号为![]() ,它们将圆周分成800个间隙.今选定某一点染成红色,然后按如下规则,逐次染红其余的一些点:如果第
,它们将圆周分成800个间隙.今选定某一点染成红色,然后按如下规则,逐次染红其余的一些点:如果第![]() 号点已被染红,则可按顺时针方向转过
号点已被染红,则可按顺时针方向转过![]() 个间隙,再将所到达的那个端点染红.如此继续下去.试问圆周上最多可得到多少个红点?证明你的结论.
个间隙,再将所到达的那个端点染红.如此继续下去.试问圆周上最多可得到多少个红点?证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】边长为1的菱形![]() 的两对角线交于
的两对角线交于![]() ,过
,过![]() 作A2B2∥A1B1交
作A2B2∥A1B1交![]() 于
于![]() 连结
连结![]() 交
交![]() 于
于![]() ,过
,过![]() 作A3B3∥A1B1交
作A3B3∥A1B1交![]() 于
于![]() ,…,这样作下去得
,…,这样作下去得![]() 以
以![]() 为原点,
为原点,![]() 所在直线为
所在直线为![]() 轴,建立平面直角坐标系,设以
轴,建立平面直角坐标系,设以![]() 为半径,圆心在
为半径,圆心在![]() ,轴上的一列圆
,轴上的一列圆![]() 依次相外切(即
依次相外切(即![]() 与
与![]() 外切,
外切,![]() ),若圆T1与抛物线
),若圆T1与抛物线![]() 相切.求证:所有的圆
相切.求证:所有的圆![]() 都与抛物线
都与抛物线![]() 相切.
相切.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等比数列{an}的各项均为正数,且2a1+3a2=1, ![]() =9a2a6.
=9a2a6.
(1)求数列{an}的通项公式;
(2)设bn=log3a1+log3a2+…+log3an,求数列![]() 的前n项和.
的前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知Sn为数列{an}的前n项和,且Sn+2=2an,n∈N*.
(1)求数列{an}的通项公式;
(2)令bn![]() ,设数列{bn}的前项和为Tn,若Tn
,设数列{bn}的前项和为Tn,若Tn![]() ,求n的最小值.
,求n的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
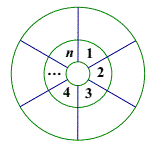
【题目】如图所示将同心圆环均匀分成n(![]() )格.在内环中固定数字1~n.问能否将数字1~n填入外环格内,使得外环旋转任意格后有且仅有一个格中内外环的数字相同?
)格.在内环中固定数字1~n.问能否将数字1~n填入外环格内,使得外环旋转任意格后有且仅有一个格中内外环的数字相同?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com